Salut a tous,
Dans cet article je vais vous expliquer comment effectuer des calculs avec les grands nombres ( plutot les tres grands nombres). La grandeur de ces nombres sera seulement limitee par la memoire disponible sur votre ordinateur ! ;) J’en vois deja qui se disent : super je vais pouvoir calculer les 1000 premieres decimales de PI. ;)
Certains d’entre vous peuvent se demander pourquoi j’ai decide d’elaborer un tel article ?
Tout d’abord il est tres interessant de mettre en place une librairie permettant d’effectuer ce type de calcul. D’autre part lorsque j’aurai termine ma serie d’article sur ce sujet je vais ecrire une serie d’articles sur la cryptographie afin de vous apprendre a proteger vos programmes.
Bon rentrons dans le vif du sujet. Pour ce premier article j’ai decide de commencer par les bases : soit l’addition, la soustraction, la multiplication, la division ( reste + diviseur) avec des nombres positifs.( ce qui represente deja beaucoup)
Je suppose que certains d’entre vous ont deja essaye de mettre en place une telle librarie et je suis a peu pres sur que de nombreuses personnes ont tout simplement utilise une librairie adaptee comme Bignum sans rien y comprendre. Cette article va donc, je l’espere, vous permettre de comprendre et de realiser ce type de librairie.
| >Comment utiliser des grands nombres |
| >Resolution du " probleme " |
De nos jours les registres de calcul de nos processeurs sont limites a 32Bits. Certains compilateurs permettent de realiser des calculs sur 64Bits. Mais selon mon point de vue la limite de 64 Bits peut facilement devenir un inconvenient ( bien que 2^64=18446744073709551616 ).
Dans la vie de tous les jours nous representons nos nombres avec des chiffres appartenant à [0 ; 9]. On parle alors de nombres ecrits en base 10.
Soit n un entier naturel ( c’est à dire un entier positif : 0 1 2 3 4 5 6 7 8 9 10 11 ... )
En base N un nombre s’ecrit :
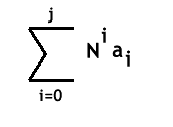
Avec ai un chiffre defini en fonction de i appartenant à [0 ; N [ et j un nombre tel que tous les ai associés à un i > j soit egaux à 0.
Exemple : 1121= 1.10^0 + 2.10^1 + 1.10^2 + 1.10^3 (d’ou son ecriture en base 10)
Maintenant la notion de base est definie ! C’etait pas tres complique.
Pour permettre a un maximum de type de processeurs d’effectuer des calculs avec les grands nombres j’ai decide d’utiliser la base 256. Ainsi tous les processeurs pouvant realiser des calculs sur 16 Bits pourront etre utilise. (Oui 16 Bits et non 8 Bits vous comprendrez plus loin pourquoi).
Ainsi les grands nombres seront sous la forme :
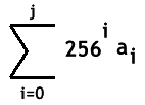
Avec ai appartenant à [0 ; 255]
Comme nous avons determine de quelle maniere nous allons representer les grands nombres nous allons pouvoir passer a la premiere operation arithmetique : l’addition.
Je tiens a signaler que je vais tout d’abord m’occuper des nombres positifs. Puis lorsque j’aurai elabore des algorithmes permettant d’effectuer des additions, soustractions, multiplications et divisions je generaliserais ces operations aux entiers relatifs (nombres postifis et negatifs). (pour les nombres negatifs se sera pour le prochain numero).
| >Définition d’un nouveau type pour la programmation |
Du point de vue de la programmation dans cet article les listings seront rediges en C et pour une meilleur comprehension je n’utiliserai pas de pointeurs mais des tableaux " predefinis ". Evidemment je vous conseille de passer, une fois tout l’article compris, aux pointeurs car le programme sera plus rapide ( ce qui est tres important ;) ;) ) et ne sera pas limite en ce qui concerne la taille des grands nombres !
J’ai donc decide de mettre en place un type ( et non une classe : j’elaborerai une classe lorsque toute la serie d’articles sur ce sujet sera " terminee ") .
Donc voici le type bignb :
typedef struct bignb {
int signe; //signe du nombre (0 = positif et -1 = negatif)
int nb; //nombre de chiffres (en fait nombre de chiffres -1)
unsigned int nomb[200]; //tableau contenant les chiffres du nombre
//(on peut observer ici la limite de calcul cite precedemment)
} bignb;
| l |
| >L’addition |
L’addition est une operation elementaire. Elle represente une excellente initiation au calcul avec les grands nombres compte tenu de sa grande simplicite.
| >Presentation de l’algorithme |
Tout d’abord je tiens a vous dire que j’ai du trouve par moi-meme l’ensemble des algorithmes utilises dans cet article : j’ai essaye d’elaborer des algorithmes suffisamment rapide mais il existe surement des algorithmes plus rapides que ceux-ci. Si vous connaissez des algorithmes plus performant faites les moi parvenir à loubail@club-internet.fr (LIEN)
L’algorithme utilise pour l’addition est veritablement simple. Il suffit d’additionner les chiffres de 2 nombres en base 256 un a un de la meme maniere qu’en base 10. Evidemment il y a le probleme avec la retenue. Comment proceder ?
C’est ici que la remarque faite precedemment : (Oui 16 Bits et non 8 Bits vous comprendrez plus loin pourquoi) prend son importance.
Soit nb1 et nb2 deux grands nombres. Soit nb3 un grand nombre tel que nb3=nb1+nb2
On effectue tout d’abord l’addition membre a membre des chiffres de nb1 et de nb2 ce qui donne : Avec nb1i et nb2i les chiffres de nb1 et nb2 associes a i et j le nombre de chiffres du nombre le plus grand entre nb1 et nb2.
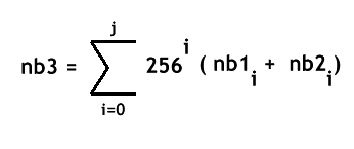
Ensuite il faut effectuer une sorte de remise en forme. Je m’explique : lorsque vous additionnez deux nombres appartenant à [0 ; 255] (8Bits) le résultat appartient à [0 ; 510]. (16 Bits). (D’où l’importance de la remarque citée precedemment !)
Comment effectuer une telle remise en forme ?
Pour se faire je vais utiliser les congruences. Quoi les congruences c’est quoi ce machin ? Eh bien c’est simple (si on veut ! ;) )
Avant tout pour comprendre ce qu’est la congruence il faut parler de division euclidienne. Je ne vais effectuer aucune demonstration mathematique, vous devrez admettre ceci :
Soit a un entier naturel et b un entier naturel non nul. Alors il existe un unique couple (q ;r) d’entiers naturels verifiant a=bq + r et r appartient a [0 ;b[. Ceci definit la division euclidienne dans N (l’ensemble des entiers naturels). (NDLR: q est appelé quotient et r reste) | l |
Maintenant voici ce que vous devez admettre en ce qui concerne les congruences :
Definition : Soit n un entier naturel superieur ou egal a 2. Deux entiers a et a’ qui ont le meme reste dans la division euclidienne par n sont dits congrus modulo n. On ecrit a | l |
Bon ben on fait quoi avec ca ? Eh ben on va pouvoir remettre en forme nb3.
Comme nb3 doit etre ecrit en base 256 on va effectuer des congruences modulo 256. Chaque chiffre sera verra affectee une valeur V tel que V
 nb3i (modulo 256).
Ensuite si nb3i/256 = 1 on ajoutera au nombre nb3i+1 la valeur 1.
En somme on obtient l’algorithme suivant j fois (j etant le nombre de chiffre de nb3):
nb3i (modulo 256).
Ensuite si nb3i/256 = 1 on ajoutera au nombre nb3i+1 la valeur 1.
En somme on obtient l’algorithme suivant j fois (j etant le nombre de chiffre de nb3):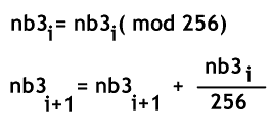
Apres avoir applique cet algorithme il se peut que le nombre de chiffre de nb3 est change s’il y a eu une retenu sur le dernier chiffre.
Donc on effectue le test suivant :
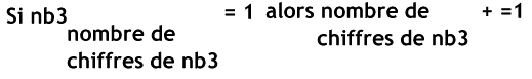
| >Exemple concret |
Je vais effectuer un exemple avec des nombres petits (mais pas trop quand meme) pour que vous puissiez verifier sur votre calculatrice (Ti, Casio, HP (j’utilise une HP48 ;) )) ou un logiciel de calcul mathematique (gardez Maple pour plus tard j’en parlerai plus loin dans cet article !))
Bon je pose nb1= 138.256^0 + 18.256^1 + 121.256^2 + 221.256^3
Et nb2= 47.256^0 + 123.256^1 + 145.256^2
Donc nb1 dispose de 4 chiffres et nb2 de 3 chiffres.
Ainsi je vais effectuer deja 4 calculs.
nb3.nomb[0] = nb1.nomb[0]+nb2.nomb[0] = 185; nb3.nomb[1] = nb1.nomb[1]+nb2.nomb[1] = 141; nb3.nomb[2] = nb1.nomb[2]+nb2.nomb[2] = 266; nb3.nomb[3] = nb1.nomb[3]+nb2.nomb[3] = 221; | l |
Et ensuite la remise en forme
nb3.nomb[0] = nb3.nomb[0] (modulo 256) = 185; nb3.nomb[1] = nb3.nomb[1] (modulo 256) = 141 ; nb3.nomb[2] = nb3.nomb[2] (modulo 256) = 10 ; Comme 266/256=1 nb3.nomb[3]=nb3.nomb[3]+1=222 : nb3.nomb[3] = nb3.nomb[3] (modulo 256) = 222 ; | l |
Donc nb3=185.256^0 + 141.256^1 + 10.256^2 + 222.256^3
| >Optimisation |
Je vais desormais optimiser cet algorithme en fusionnant les deux processus : celui d’addition puis celui de remise en forme en un seul processus. (Je parle d’optimisation mais je tiens a preciser que ceci n’est pas une veritable optimisation au sens premier du mot !)
On garde toujours nb1 et nb2, et nb3 comme resultat de nb1 + nb2
Et bien on applique ceci :
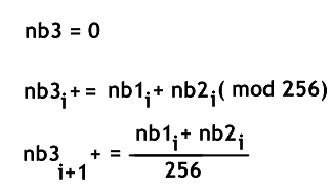
Comme vous pouvez le constater il faut affecter à nb3 la valeur 0 avant l’application de cet algorithme comme on ajoute a la valeur nb3i une autre valeur.
| >Programmation |
bignb addition(bignb nb1,bignb nb2)
{
int i,j;
bignb nb3=zeronb(); // nb3=0 ; je parle de cette fonction plus loin dans l’article
if(nb1.nb>nb2.nb)
j=nb1.nb //on affecte à j la plus importante valeur de nombre de chiffre
else
j=nb2.nb;
nb3.nb=j; //le nombre de chiffres de nb3 est egal a j
for(i=0;i<=j;i++)
{
nb3.nomb[i]+=(nb1.nomb[i]+nb2.nomb[i])%256; //algorithme presente au c)
nb3.nomb[i+1]+=(nb1.nomb[i]+nb2.nomb[i])/256;
}
if(nb3.nomb[nb3.nb+1]!=0) nb3.nb++; //on regarde s’il ne faut pas incremente le nombre
//de chiffre de nb3
return(nb3); //on quitte la procedure et on retourne a l’appelant nb3
}
| l |
| >La multiplication |
Bon nous allons desormais passer a quelque chose d’un petit peu plus complique.
- Une solution evidente :
Avant de commencer a vous presente cette solution je tiens a vous signale que ce n’est pas une solution " intelligente " : vous allez rapidement comprendre pourquoi.
Soit nb1 et nb2 deux chiffres. Soit nb3 le resultat de nb1 * nb2.
La solution evidente consisterait donc a realise nb1 fois l’operation nb2+nb2.
Si on repete nb1 fois nb2+nb2 et si nb1 et nb2 possedent 300 chiffres ceci risque d’etre tres long en terme de " cycles processeurs ".
- Une solution plus appropriee :
Au lieu de faire des grandes phrases je vais poser des calculs :
On pose nb1 = a0 + a1.256 + a2.256^2 + a3.256^3 ... et nb2 = b0 + b1.256 + b2.256^2 + b3.256^3 ... nb3 = nb1 * nb2 = ( a0 + a1.256 + a2.256^2 + a3.256^3 ... ) * ( b0 + b1.256 + b2.256^2 + b3.256^3 ... ) = a0 * ( b0 + b1.256 + b2.256^2 + b3.256^3 ... ) + a1.256 * ( b0 + b1.256 + b2.256^2 + b3.256^3 ... ) + a2.256^2 * ( b0 + b1.256 + b2.256^2 + b3.256^3 ... ) + a3.256^3 * ( b0 + b1.256 + b2.256^2 + b3.256^3 ... ) ...l
Voilà cette derniere ligne de calcul est tres interessante afin de mieux comprendre le processus ( si vous ne l’avez pas encore compris ;) ) je vais vous presenter le calcul sous une autre forme.
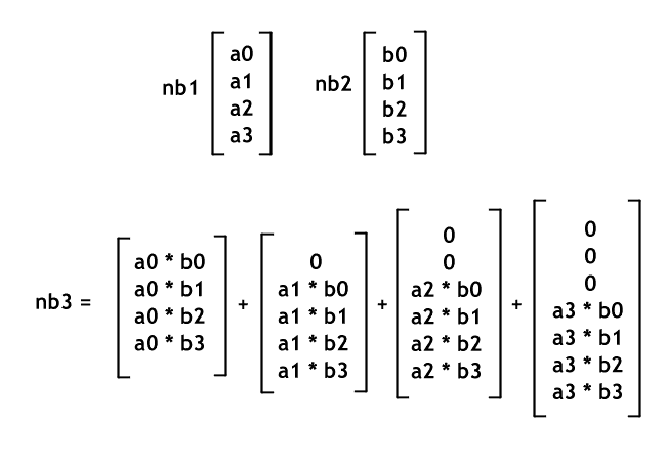
Selon mon point de vue cette representation est plus simple a comprendre et resume bien le principe que nous allons incorpore dans notre algorithme.
L’algorithme que nous allons utilise va donc tout d’abord elaborer j " tableaux ".
Chaque tableau representera un grand nombre.
Soit Tab le groupe de tableau et i l’indice du tableau considere. On aura ainsi nb3 = nb1 * nb2 = Tab0 + Tab1 + Tab2 + Tab3 ...
Avec Tab0 = a0 * nb2 , Tab1 = a1.256 * nb2, Tab2 = a2.256^2 * nb2, Tab3 = a3.256^3 * nb2, ...
Ceci effectue il faudra remettre en forme les nombres associe aux tableaux comme lors de l’addition puis additionner ces nombres entre eux. On obtiendra alors nb3, le resultat de nb1 * nb2.
Combien de tableaux doivent etre utilises pour un tel calcul ?
Il evident que nous envisageons d’utiliser le moins de tableaux possibles. Donc on pose j le nombre de chiffres du nombre le plus petit entre nb1 et nb2. On utilisera alors j tableaux.
Pourquoi j tableaux ? Et bien tout simplement parce que j calculs prendront place ! Je ne vais pas perdre mon temps a vous expliquer pour quelle raison j calculs prennent place car je considere que ceci est evident ( et meme si toute evidence merite d’etre demontree ;) ).
Donc apres avoir etabli nos tableaux il faut faire en sorte, comme lors de l’addition, que tous les chiffres du nombre associe au tableau appartiennent a [0 ; 255]. Etant donne que j’ai deja parle de cette methode plus haut il n’est pas necessaire de rentrer dans les details. Je rappelle seulement pour les personnes qui l’auraient oublie qu’on utilise des congruences modulo 256.
Enfin on effectue l’addition de tous les tableaux apres avoir effectue leur remise en forme.
L’algorithme que nous allons utilise sera legerement different de celui ci car il effectuera a la fois les multiplications intermediaires et les remises en forme comme lors de l’addition.
| >Exemple concret : |
nb1 = 18.256^0 + 121.256^1 + 21.256^2
nb2 = 118.256^0 + 134.256^1 + 121.256^2
nb3 = nb1*nb2
= 18 (118.256^0 + 134.256^1 + 121.256^2) +121.256*(118.256^0 + 134.256^1 + 121.256^2) +
21.256^2*(118.256^0 + 134.256^1 + 121.256^2)
= (2124 + 2412.256^1 + 2178.256^2) + (14278.256^1 + 16214.256^2 + 14641.256^3) + (
2478.256^2 + 2814.256^3 + 2541.256^4)
= ( 76 + 116.256 + 139.256^2 + 8.256^3) + ( 198.256 + 141.256^2 + 112.256^3 + 57.256^4) + (
174.256^2 + 7.256^3 + 248.256^4 + 9.256^5)
= 76 + (116 + 198).256 + (139 + 141 + 174).256^2 + (8 + 112 + 7).256^3 + (57 + 248).256^4 +
9.256^5
= 76 + 314.256 + 454.256^2 + 127.256^3 + 305.256^4 + 9.256^5
= 76 + 58.256 + 199.256^2 + 128.256^3 + 49.256^4 + 10.256^5
| l |
Ouf ! ! ! ;) C’est termine ! Nous pouvons desormais passe de la " theorie " a la pratique par la programmation. (Enfin ! ;) )
| >Programmation |
Etant donne que je viens de vous presente l’algorithme a utiliser je vais seulement annote succintement les lignes de code.
bignb multiplication(bignb nb1,bignb nb2)
{
int i,j;
int nbch; // nbch est le nombre de calculs
bignb nb3; // nb3 constituera le resultat de l’operation
bignb nb4[100]; // les tableaux pour les operations intermediaires
if(nb1.nb>nb2.nb) // on fait en sorte que le nombre de chiffre de nb2 soit plus
{ // grand que le nombre de chiffre de nb1
nb3=nb1;
nb1=nb2;
nb2=nb3;
}
nbch=nb1.nb; // nbch = nombre de chiffres de nb1
for(i=0;i<=nbch;i++) // on effectue nbch calculs
{
for(j=0;j<=nb2.nb+i+1;j++) nb4[i].nomb[j]=0; // comme lors de l’addition et pour les memes
// raisons il faut que toutes nb4 = 0
for(j=i;j<=nb2.nb+i;j++) // on laisse i 0 qui correspondent a la multiplication par 256^i
{
nb4[i].nomb[j]+=(nb2.nomb[j-i]*nb1.nomb[i])%256; // multiplication + remise en forme
nb4[i].nomb[j+1]+=(nb2.nomb[j-i]*nb1.nomb[i])/256; // multiplication + remise en forme
}
nb4[i].nb=nb2.nb+i; // le nombre de chiffres de i est egal au nombre de chiffre de nb2 plus
// le nombre de 0 associe a la multiplication par 256^i
if(nb4[i].nomb[nb4[i].nb+1]!=0) nb4[i].nb++; // on regarde comme lors de l’addition s’il ne
// faut pas incremente la valeur du nombre de chiffre de nb4
}
for(i=0;i<=nbch;i++) nb3=additio(nb4[i],nb3); // ensuite on additionne tous les tableaux
return(nb3); //on quitte la procedure et on retourne a l’appelant nb3
}
| l |
| >La soustraction |
| >Solution |
On passe desormais a une autre operation elementaire : la soustraction.
Comme, pour le moment on ne s’occupe que de nombres positifs nous allons faire en sorte que le resultat soit positif.
Le gros probleme de cette operation reside dans les retenues : dans certains cas il ne faut pas oublier de " propager " une retenue.
Soit nb1 et nb2 deux nombres tels que nb1>=nb2 et nb3 le resultat de nb1 - nb2
nb1 = a0 + a1.256 + a2.256^2 + a3.256^3 ... et nb2 = b0 + b1.256 + b2.256^2 + b3.256^3 ...
nb3 = (a0-b0) + (a1-b1).256 + (a2-b2).256^2 + (a3-b3).256^3 ...
Durant le calcul de nb3 differents se presentent :
- si on a ai-bi >=0 soit ai>bi alors le calcul de nb3 s’effectue sans aucun probleme
- si on a ai<bi pour plusieurs i alors deux cas se presentent :
- si ai+1-bi+1 >= 0 alors nb3i = ai-bi + 256 et nb3+1=ai-bi-1
- si ai+1-bi+1 < 0 alors on etabli une boucle qui propage la retenue j fois jusqu’à ce que aj - bj >= 0
A ceux qui n’ont rien compris : ne vous affolez pas, je vais donner des exemples concrets.
| >Exemples concrets |
Premier cas :
Pour tout i ai >= bi
nb1 = 121 + 37.256 + 14.256^2 +154.256^3
nb2 = 18 + 5.256 + 7.256^2 + 121.256^3
nb3 = nb1 - nb2
= (121-18) + (37-5).256 + (14-7).256^2 + (154-121).256^3
= 103 + 32.256 + 7.256^2 + 33.256^3
| l |
Deuxieme cas :
ai < bi et ai+1 >= bi+1
nb1 = 121 + 37.256 + 2.256^2 +154.256^3
nb2 = 18 + 5.256 + 7.256^2 + 121.256^3
nb3 = nb1 - nb2
= (121-18) + (37-5).256 + (2-7).256^2 + (154-121).256^3
= 103 + 32.256 + (2-7 + 256).256^2 + (154-121 - 1).256^3
= 103 + 32.256 + 251.256^2 + 32.256^3
| l |
Troisieme cas :
ai < bi et ai+1 > bi+1 nb1 = 11 + 2.256 + 2.256^2 +154.256^3 nb2 = 18 + 5.256 + 7.256^2 + 121.256^3 | l |
Ici a0<b0 et a1<b1 et a2<b2 et a3>=b3 Une propagation de retenue est necessaire !
nb3 = nb1 - nb2
= (11-18) + (2-5).256 + (2-7).256^2 + (154-121).256^3
= (11-18 + 256) + (2-5 - 1).256 + (2-7).256^2 + (154-121).256^3
= (11-18 + 256) + (2-5 - 1 + 256).256 + (2-7 - 1).256^2 + (154-121).256^3
= (11-18 + 256) + (2-5 - 1 + 256).256 + (2-7 - 1 + 256).256^2 + (154-121 - 1).256^3
= 249 + 252.256 + 250.256^2 + 32.256^3
| l |
J’espere que ces exemples vous ont permi de mieux assimile l’algorithme utilise.
| >Programmation |
//Soustraction de grands nombres
bignb soustractio(bignb nb1,bignb nb2)
{
int i,j;
bignb nb3; // le resultat
if(comp(nb1,nb2)==-1) //compare nb1 et nb2 si nb1 | l |
| >Division et reste |
- Solution evidente :
Comme lors de la multiplication une solution evidente mais tres peu efficace peut etre envisagee. Il suffirait d’effectuer n soustractions jusqu'à obtenir un reste inferieur au diviseur.
Pour des raisons similaires de celles precisees lors de la multiplication cette solution est a exclure.
- Une solution plus appropriee :
Apres mures reflexions j’ai elabore un algorithme plutot satisfaisant. Je ne vais pas vous cacher qu’il est plus complique que ceux que nous avons vu jusqu'à present.
Soit nb1 et nb2 deux grands nombres nb1/nb2=a*nb2 +b ; (Cf debut de l’article : division euclidienne) avec a le quotient et b le reste
l
Tout d’abord il faut traiter des cas evidents :- Si nb1 < nb2 alors a=0 et b = nb1
- Si nb2=1 alors a=nb1 et b=0
- Si nb2=0 alors on admet que a=0 et b=nb1
Desormais nous pouvons passer au cas general, qui est beaucoup plus interessant et complique. ;)
On a nb1>=nb2. Soit vald un nombre tel que vald>nb2.nomb[nb2.nb] (je rappelle au passage que nb2.nb=nombre de chiffre de nb2 - 1). Plus precisement val est tel que vald=(nb2.nomb[nb2.nb]+1). Par exemple si nb2=13.256^2 + 125.256 + 11 alors vald=14.
On pose : nb3=nb1. Ensuite on effectue la difference entre le nombre de chiffre de nb3 et le nombre de chiffre de nb2. (Vous allez comprendre pourquoi !). Soit j3 cette difference. Soit muld un nombre qui representera le quotient.
Debut de l’algorithme :
Soit mula un nombre defini par mula=(nb3.nomb[nb3.nb]/vald)*256^j3. On a desormais des valeurs tres interessantes. Pourquoi, me direz-vous ?
Lorsque vous divisez nb1 par nb2 et que nb1 > nb2 alors on peut au moins soustraire a nb1 z fois la valeur de nb2. (z etant defini comme la division de nb1 par un nombre plus grand que nb2).
En partant de ce principe on calcule un z assez proche de la valeur de a que l’on cherche d’ou l’utilite de vald puis de mula.
Lorqu’on a calcule mula plusieurs cas se presentent :
- Si le dernier chiffre de mula, soit le quotient dans la division de nb3.nomb[nb3.nb] par vald, vaut
zero alors mula est trop grand
On decremente alors la valeur de j3 et on definit mula de la facon suivante : mula.nomb[j3]= ( (nb3.nomb[nb3.nb-1]+256*nb3.nomb[nb3.nb])/vald ) *256^j3
Ensuite on remet en forme mula afin que tous les chiffres de mula appartiennent à [0;255].
Quel en est l’interet ? Comme on a pris un z trop grand on en cherche un plus petit. ;) Apres avoir realise ceci des tests doivent etre effectues.
- Si le nombre de chiffre de nb3 - 1 est inferieur au nombre de chiffre de nb2 alors ce qui a ete opere au dessus est faux. En effet dans ce cas nb2 diviserait un nombre plus petit que lui-meme. Ainsi comme nb3>nb2 mula=1. Ceci permettra d’effectuer : nb3=nb3-nb2
- Si mula=0, comme nb3>nb2 on pose egalement mula=1
- Sinon on continue sans operer de modifications
Ensuite on pose nb5=mula*nb2
muld=muld+nb5 ( -> on ajoute a muld la nouvelle valeur que l’on soustrait a nb3 ) nb3=nb3-nb5 on compare alors nb3 et nb2 si nb3<nb2 alors on a reussi ;) si nb3==nb2 alors on a egalement reussi et on pose nb3=0 si on a reussi alors b=nb3 et a=muld et on n’arrete d’appliquer l’algorithme sinon on reapplique cet algorithme depuis Debut de l’algorithme : | l |
| >Type specifique a la division |
J’ai defini un type nouveau pour le resultat d’une division : le type bigdiv
typedef struct bigdiv {
bignb bgdiv; //le diviseur
bignb bgrest; //le reste
} bigdiv;
| l |
| >Exemple concret |
Une exemple semble etre le bien venu ! ;)
nb1=17+113.256+221.256^2+42.256^3
nb2=145+78.256
muld=0
vald=79
42/79=0
mula=0.256^2
221+42*256=10973
10973/79=138
mula=138.256
nb5=(138.256)*(145+78.256)
nb5=42.256+90.256^2+42.256^3
muld=138.256
nb1=nb1-nb5=17+71.256+131.256^2
131/79=1
mula=256
nb5=145.256+78.256^2
muld=139.256
nb1=nb1-nb5=17+182.256+52.256^2
52/79=0
mula=0
182+52*256=13494
13494/79=170
mula=170
nb5=(145+78.256)*170
nb5=74+44.256+52.256^2
muld=170+139.256
nb1=nb1-nb5=199+137.256
137/79=1
mula=1
nb5=145+78.256
muld=171+139.256
nb1=nb1-nb5=54+59.256
Donc nb1= (171+139.256) * nb2 + (54+59.256)
| l |
J’espere que cet exemple vous aura permis de mieux comprendre cet algorithme.
| >Programmation : |
Cette fois-ci je vous met le code sans de nombreuses annotations car je pense qu’il n’y a rien a ajoute quand a la comprehension de l’algorithme et donc du code
Le seul point qui pourrait vous paraître obscure est la forme de mula et muld : comme mula et muld doivent etre des grands nombres il faut definir leur nombre de chiffre et mettre des 0 ou il faut ! ;)
bigdiv reste(bignb nb1,bignb nb2)
{
int i,j,j2,j3,j4,vald;
bignb nb3,nb4,nb5;
bignb mula;
bignb muld=zeronb();
bigdiv result;
int varcomp=0; //pour comparer nb2 et nb3
int varcomptps;
//****************
//* Cas evidents *
//****************
if(comp(nb1,nb2)==-1)
{
result.bgdiv.nb=0;
result.bgdiv.nomb[0]=0;
result.bgrest=nb1;
return(result);
}
if(nb2.nb==0) if(nb2.nomb[0]==0)
{
result.bgdiv.nb=0;
result.bgdiv.nomb[0]=0;
result.bgrest=nb1;
return(result);
}
if(nb2.nb==0) if(nb2.nomb[0]==1)
{
result.bgrest.nb=0;
result.bgrest.nomb[0]=0;
result.bgdiv=nb1;
return(result);
}
//****************
//* Sinon l'algo *
//****************
vald=nb2.nomb[nb2.nb]+1;
nb3=nb1;
while(varcomp!=-1) //tant que nb1>nb2
{
j3=nb3.nb-nb2.nb;
mula.nb=j3;
for(j=0;j<=j3;j++) mula.nomb[j]=0;
mula.nomb[j3]=nb3.nomb[nb3.nb]/vald; //Cf algorithme
if(mula.nomb[j3]==0)
{
//Cf algorithme
j3=nb3.nb-nb2.nb-1;
mula.nb=j3;
for(j=0;j<=j3;j++) mula.nomb[j]=0;
mula.nomb[j3]=((nb3.nomb[nb3.nb-1]+256*nb3.nomb[nb3.nb])/vald)%256;
mula.nomb[j3+1]=((nb3.nomb[nb3.nb-1]+256*nb3.nomb[nb3.nb])/vald)/256;
if(mula.nomb[j3+1]!=0)
{
mula.nb++;
j3++;
}
if(nb3.nb-1<nb2.nb)
{
mula.nb=0;
j3=0; //nb3.nb-nb2.nb;
mula.nomb[j3]=1;
}
if (mula.nomb[j3]==0)
mula.nomb[j3]=1;
}
muld=additio(muld,mula);
nb5=multiplicatio(mula,nb2);
nb3=soustractio(nb3,nb5);
varcomptps=comp(nb3,nb2);
if(varcomptps<=0) varcomp=-1;
if(varcomptps==0) nb3=zeronb();
}
result.bgdiv=muld;
result.bgrest=nb3;
return(result);
}
| l |
| >Comparaison de deux grands nombres |
| >Algorithme |
La comparaison de deux grands est relativement aisee.
Soit nb1 et nb2 deux grands nombres
- Si nb1.nb>nb2.nb nb1>nb2
- Si nb1.nb<nb2.nb nb1<nb2
- Si nb1.nb==nb2.nb on doit comparer tous les chiffres de nb1 et nb2 1 a 1 en commencant par les derniers jusqu'à trouver un chiffre superieur a l’autre ce qui permettra de determiner le nombre le plus grand entre nb1 et nb2.
| >Programmation |
Voici la fonction a laquelle je faisais reference precedemment.
- Si nb1>nb2 alors on retourne 1 a l’appelant
- Si nb1<nb2 alors on retourne -1 a l’appelant
- Si nb1=nb2 alors on retourne 0 a l’appelant
int comp(bignb nb1,bignb nb2)
{
int i;
if(nb1.nb>nb2.nb) return(1);
if(nb1.nb<nb2.nb) return(-1);
for(i=nb1.nb;i>=0;i--)
{
if(nb1.nomb[i]>nb2.nomb[i]) return(1);
if(nb1.nomb[i]<nb2.nomb[i]) return(-1);
}
return(0);
}
| l |
| >Mise a zero de grands nombres |
| >Programmation |
Un nombre egal a 0 est positif et comporte 1 chiffre. Notre grand nombre prendra donc les parametres suivants :
nb=0 signe=0 | l |
Et on devra mettre a zero tous les chiffres du tableau nomb
bignb zeronb(void)
{
int i;
bignb nb1;
nb1.nb=0;
for(i=0;i<200;i++) nb1.nomb[i]=0;
nb1.signe=0;
return(nb1);
}
| l |
| >Conclusion |
Ce premier article sur les calculs avec les grands nombres est termine. Nous avons ainsi elabore des fonctions permettant d’effectuer les 4 operations arithmetiques les plus elementaires avec des nombres positifs. Les prochains articles generaliseront ces calculs aux nombres negatifs decriront un algorithme qui permet d’afficher les grands nombres a l’ecran (passage de la base 256 a la base 10), s’interesseront au pgcd, a bezout, a l’inverse modulo, a la puissance modulo b, etc ...
J’espere avoir ete suffisamment clair. Si vous voulez me poser des questions, si vous avez des remarques, si vous voulez me donner votre avis sur cet article ecrivez-moi a : loubail@club-internet.fr(LIEN) ou bailsite@hotmail.com(LIEN)
Vous pouvez aussi visiter mon site : http://www.multimania.com/loubail/ (Site en francais - LIEN) ou http://www.geocities.com/SiliconValley/Chip/8195 (Site en anglais - LIEN).