Mon centre d'intérêt: tracer un cercle ou une ellipse sans utiliser les réels et en expliquant tout sans faire d'ellipse et sans chercher la quadrature du cercle. J'ai consulté le cercle de mes amis (le seul qui ne tourne pas rond), dans lequel chacun se fait des ronds de jambe. Mais je suis resté comme deux ronds de flans, car ces ronds de cuir ne m'ont rien appris, c'est un cercle vicieux. Sous les rayons de soleil, mon rayon visuel est tombé sur le rayon d'une librairie (au centre de celle-ci). J'ai fait les yeux ronds en voyant le chiffre rond du prix du livre. Je n'avais pas un rond. Le chef de rayon, déjà rond comme une queue de pelle, m'a envoyé de son gros ventre rond, faire une ronde hors de son rayon d'action, tout en sifflant quelques notes (noires, blanches et rondes). Je vous livrerai toutefois, de mon écriture ronde, mes connaissances à décortiquer aux rayons X. Ne poussez pas des cris d'éléphants (bary-centre), il y a centre et-pis-centre
| >0) Introduction. |
| l | Cet article fait suite au tracé de droites paru dans le précédent prograzine (LIEN). Les tracés de cercles et de droites utilisent une démarche et des astuces semblables, et la compréhension des droites peut grandement aider pour ingurgiter cet article. |
| >0-0) Cercles ou ellipses? |
Je m'interesse ici surtout aux tracés de vrais cercle à l'écran, ou tout du moins à une figure rapide à tracer qui s'en approche. Le résultat ne peut être parfait, du fait de la discontinuité des points d'une part, et du fait que la largeur et la hauteur de l'ecran est réglable d'autre part. En effet pour tracé un cercle "parfait" à l'ecran, il serait nécéssaire d'étalloner le tracé d'un carré ou d'un cercle. L'étallonnage cesse sa validité si on change d'ordinateur ou si on modifie les réglages de l'écran.
En mode 640x480 ou en mode X, les pixels sont à peu près carrés. On se simplifira la vie en utilisant les procédures de tracés de cercles. Ceux-ci sont largement décrits sur le net, même si le choix de l'algorithme n'est pas, de mon goût, toujours le meilleur.
En mode 13h, le rapport hauteur/largeur est assez voisin de 1,2. Il nous faudra donc tracer des ellipses malgré les deux inconvéniants que cela entraîne: calculs plus complexes (plus longs) et dissymétrie du tracé si on permute les X et les Y. Si on trace un cercle, avec des approximations, il sera toujours fermé; avec une ellipse, on pourait avoir une figure ouverte.
Je n'ai pas envore vu de résolutions d'écrans avec des rapports hauteur/largeur trop différents de 1. L'algorithme avec approximation de Martin est donné pour un rapport de 1,2 mais les essais que j'ai fait m'indiquent qu'on peut aller bien au dela.
| >0-1) Un cercle de pixels. |
En informatique, il y a deux façons de tracer des cercles: le tracé vectoriel, et le tracé pixel par pixel. Cet article va donner quelques algorithmes pour le tracé par pixels.
| l | Les exigences trouvées dans le tracé de droites (continuité du tracé pour pouvoir utiliser le remplissage, pas de surépaisseur) sont toujours d'actualité. |
Les cercles (et les ellipse) sont normalement tracés par 8 arcs:
^y
\ 3 | 2 /
\ | /
\ | /
4 \ | / 1
\|/
-----*----->x
/|\
5 / | \ 8
/ | \
/ | \
/ 6 | 7 \
| l |
Pour un cercle, on calcule les points de la zone 1, et par symétrie, on trace les points des zones 1 4 5 et 8, puis par permutation de X et de Y, on trace les autres points.
En effet si on vient de calculer le point (X,Y) de la zone 1, il faut donc aussi tracer (X,-Y) pour la zone 8, (-X,Y) pour la zone 4 et (-X,-Y) pour la zone 5. Enfin pour les symétries, on trace (Y,X), (-Y,X), (Y,-X) et (-Y,-X). Dans les algorithmes que je donne, les 4 points des 4 premières zones (1, 8, 4 et 5) sont notés (Cx +/- X, Cy +/- Y), Cx et Cy étant les coordonnés du centre (on y ajoute plus ou moins X et Y). Les 4 points des 4 dernières zones (2, 3, 6et 7) sont notés (Cx +/- Y, Cy +/- X).
Pour une ellipse, on calcule en général les points de la zone 1, puis on fait les calculs de la zone 2. Un tracé d'ellipse demande deux fois plus de calculs, et est donc beaucoup plus long.
| >0-2) Tracé de demi-cercle, de quart de cercle... |
Je ne peux pas tout développer, mais pour tracer des arcs de cercles (1 à 7 zones), il suffit de ne tracer que les points des zones interessantes.
| >0-3) Choix du repère. |
Je choisis arbitrairement de donner, pour des raisons de lisibilité, des cercles et des ellipses centrés sur l'origine. Pour tracer un cercle de centre (Ox,Oy), il suffit de rajouter aux abscisses Ox, et aux ordonnées Oy.
Le rayon de mes cercles s'appellera R, et les "rayons" des ellipses R et r (R est le demi grand axe horizontal, r le demi petit axe vertical). En cas d'égalité R=r, on ne doit pas utiliser les tracés d'ellipses.
| >0-4) Sens du calcul. |
Pour dessiner un cercle ou une ellipse, on va commencer par dessiner la zone 1 en montant (on part du point (R,0)). La plupart des algorithmes montent verticalement, et quand l'erreur est trop grande, se décalent d'un pixel vers la gauche. Dans la zone 1, il faut dessiner un et un seul point par horizontale. Tous les bons algorithmes vont faire:
| l |
|
Ceci garanti d'une part la continuité (on trace un point pour chaque valeur de l'ordonnée) ainsi que la non surépaisseur (car on ne peut tracer qu'un seul point).
Si on trace des cercles, on peut s'arrêter sur la diagonale (x=y). Si par contre on trace des ellipses, on continue tant que le tracé ne fait pas de trous (la différence ancienne_abscisse - nouvelle_abscisse est nulle ou vaut 1). Dans le cas des tracés d'ellipses, il faut faire pareil avec la zone 2. L'algorithme de Martin continue le tracé dans le même sens (trigo) ce qui garantit la continuité du tracé. En effet à cause des approximations dûes aux calculs avec les entiers, il se pourait sinon que les deux arcs des zones 1 et 2 finissent à deux points différents.
| >1) Plus nul tu meurs. |
| l | Les coordonées polaires? |
Pour un cercle, les points ont pour coordonnés (R.cos(a),R.sin(a)). En faisant varier a entre 0 et 360 degrés, on devrait pouvoir tracer un cercle. Cette méthode ne doit pas être utilisée car l'angle entre deux points n'est pas constant. De plus cela nécéssite le calcul d'un sinus et d'un cosinus.
Enfin, le résultat ne peut pas être bon car rien ne nous garanti ni que la figure dessinée sera fermée, ni que l'on aura pas trop de points.
| >2) La trigonométrie. |
L'algorithme suivant est interessant parce qu'on le trouve sur le net mais il est très lent, encombrant, bref, c'est une curiosité mathématique. Je ne comprend pas ceux qui l'utilisent.
| >2-0) Formulaire. |
Traçons en rouge l'ellipse à dessiner ainsi qu'en noir les cercles de rayons R et r. Le point P à calculer à pour coordonnés (x,y). La droite passant par P est inclinée d'un angle alpha.
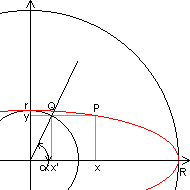
On a les relations:
- sin(alpha)=y/r
- cos(alpha)=x'/r
- x'/r=x/R
On peut en déduire x=R.cos(arcsin(y/r)) et y=r.sin(arccos(x/R)). La première formule est employée pour tracer toutes les zones en même temps pour un cercle ou les zones 1,4,5,et 8 d'une ellipse. La deuxième formule est utilisée pour tracer les zones 2, 3, 6 et 7 d'une ellipse.
| >2-1) Les réalisations. |
Je ne founirais que des remarques, cet algorithme ne m'interesse pas vraiment.
- On prends une variable "Y" et une "rapport" (elle vaut y/r). A chaque pas, on incrémente Y de 1 et rapport de 1/r.
- L'incrément 1/r étant constant, il est calculé une seule fois.
- Il vaut mieux utiliser une table de cosinus-arc-sinus. Mais le problème est de savoir combien de valeurs prendre!
- Il vaut mieux utiliser les calculs en virgule fixe.
| >3) Tracé de cercle |
La partie abordée ici s'interesse aux écrans pour lesquels les pixels sont carrés. On peut utiliser cet algorithme pour un écran quelconque mais on verra alors une ellipse. Il existe sur le net, bon nombre de site donnant des variantes de cet algorithme.
| >3-0) Equations du cercle. |
Nous avons déjà vu que l'équation paramétrique (X=R.cos(teta)...) ne donne rien de bon. Heureusement, nous avons une autre formule: un point (X,Y) du cercle vérifie X.X + Y.Y = R.R . On ne peut pas, pour un Y donné, calculer X car il y a une racine carrée (l'extraction est longue). Ce qui va nous interesser, c'est l'erreur que l'on fait si on met le point n'importe où. Reprenez la façon dont on a fait les droites: on trace une suite de pixels horizontaux et, lorsque l'erreur est trop grande, on monte d'un cran. Ici, on va faire presque pareil (pour la zone 1): on monte verticalement, et si l'erreur est trop grande, on se décale vers la gauche. Ici, on calcule l'arc de la région 1, il n'y aura pas de "pas trop inclinée" ou de "fortement inclinée". En un sens, l'algorithme de tracés de cercles est plus simple que celui de tracé de droites.
Analysons la quantité e=X.X+Y.Y-R.R . Si le point est sur le cercle, cette quantité est nulle. Pour un point à l'extérieur, la quantié est positive, et pour un point à l'intérieur de la circonférence, la quantité e est négative. Par la suite, cette quantité sera appelée erreur (d comme décision dans la littérature anglaise).
Notons tout d'abord que erreur est nulle pour le premier point tracé (R,0), sans avoir besoin de la calculer. Pour éviter de faire le calcul de trois carrés, l'algorithme de Bresenham calcule les variations de cette quantité d'un point à l'autre, et rajoute cette différence.
Supposons que pour un point tracé, j'avais une erreur donnée (notée @erreur comme ancienne-erreur); j'ai augmenté Y de 1 (dessin de l'arc 1, sens trigo). Que vaut alors erreur? Le point est (X,Y)=(X,@Y+1). Erreur vaut donc: erreur=X.X+(@Y+1)(@Y+1)-R.R soit erreur=X.X+@Y.@Y-R.R+2.@Y+1 On reconnait dedans la valeur de @erreur: erreur=@erreur+2.@Y+1 et avec la nouvelle valeur de Y (Y=@Y+1): erreur=@erreur+2Y-1.
| l | Donc: si Y augmente (de 1), erreur augmente de 2Y-1 |
On a de même, si X diminue de 1, erreur diminue de 2X+1 (a vous de faire les calculs).
| >3-1) Algorithme. |
| l | Pour tracer un cercle:
|
Merci de ne pas me poser trop de questions sur les algorithmes que vous pouvez voir ailleurs, certains ajoutent par exemple 5Y+10 (pourquoi tout est multiplié par 5?), voir même n'importe quoi (4Y+6). Je n'en suis pas responsable, merci. Quand à dire: c'est la bonne valeur puisque ça marche, c'est aussi ce que fait Martin, mais les les nombres sont plus simples et c'est dans un but de simplicité (pour aller plus vite surtout).
| >3-2) Quand l'erreur est trop grande? |
- 3-2-0) Ce qu'on voit normalement
Cette valeur viendrait de Brensenham? Bref, Si on se trompe de 1/2 pixel sur le rayon, on a X.X+Y.Y=(R+0,25)(R+0,25). L'erreur a donc augmentée de 0,5R+0,25. Dans la pratique, on calcule avec des entiers, et on se moque pas mal de 0,25 devant le rayon. On va donc faire le test erreur#supR/2. En pratique, on va, comme on avait fait avec le tracé de droite, prendre une variable erreur_moins_R_sur_2, ajouter les quantités 2Y-1 et retrancher 2X+1 et tester si cette variable est positive ou pas. Faut-il encore rappeler que R/2 s'obtient par décalage?
- 3-2-1) Pourquoi c'est faux?
Le raisonnement est complettement faux car il ne s'agit pas de savoir si le rayon est trop grand ou pas, mais de savoir si il faut ou pas décrémenter X. La meilleure méthode est de calculer l'erreur si on met le point en (X,Y) (après incrémentation systématique de Y), l'erreur si on le met en (X-1,Y) et de choisir la plus faible. Choisir la plus petite valeur absolue est pas mal, mais comme il s'agit de carrés, cela ne conduit pas toujours au meilleur choix (cependant, le mauvais choix arrive si on est proche d'un demi pixel d'erreur, ce qui n'est pas trop préjudiciable.
Si on veut faire bien, il faut donc calculer les deux erreurs et choisir. Cette méthode est longue en calculs, si bien que même Martin utilise l'autre (la fausse). Mais soyons conscients que ce n'est pas l'idéal.
| >3-3) Algorithme de Bresenham. |
| l | Pour tracer un cercle:
|
| >3-4) Approximations de Martin |
| l | Nous avons commencés par prendre n'importe quoi pour erreur, continuons! |
Remarquons que si le cercle est petit, il sera laid, et que le nombre de points à tracer sera très faible (les erreurs ne se verront pas).
Si le cercle est de bonne taille, il n'y a pas de grosse différence entre 2Y-1 et 2Y, et entre 2X+1 et 2X. En fait on "oublie" de temps en temps un "-1", mais on oublie aussi un "+1" (plus rare, il est vrai). Une autre constatation de Martin: si une droite à un défaut, cela se voit, mais pas pour un cercle. Alors allons-y, ne nous gênons pas! On va donc tout diviser par deux.
La correction de Martin consite à dire que pour les grands cercles (R#sup#sup1), il n'y a pas de problèmes, mais pour les petits cercles, on calcule une erreur trop petite de 1/2 à chaque fois (on ajoute Y au lieu de Y+1/2). Il faut donc diminuer l'erreur au départ puis qu'on ne peut pas le faire après (ce n'est plus des maths, c'est de l'info). On initialisera erreur avec -R/2 au lieu de -R/4. Rapelez vous que l'on a tout divisé par deux.
L'algorithme devient:
| l | Pour tracer un cercle:
|
Peut-on faire plus simple? Cela me parait difficile!
| >4) Tracé de vrais cercles ou de fausses ellipses. |
| >4-0) Introduction. |
L'intérêt du mode X est justement que les cercles sont des cercles, mais l'algorithme d'affichage des points lui fait parfois préférer le mode 13h dans lequel il faut dessiner des ellipses. Je ne cherche pas à dessiner des ellipses en tant que tel, même si l'algorithme que je vais vous donner permet sans doute de le faire. Avec mes maigres recherches, je n'ai pas trouvé de sites ni en anglais, ni en français, traitant des ellipses. Je m'appuierai sur de veux documents que j'ai récupérés hors net.
| >4-1) L'équation de l'ellipse. |
Il semblerait que la propriété d(F1,P)+d(F2,P)=Constante (d est la distance, P un point de l'ellipse, F1 et F2 les foyers), ne donne pas satisfaction, à cause de l'addition des distances.
Nous allons utiliser la formule: X.X/R.R + Y.Y/r.r = 1 ou plutot X.X.r.r+Y.Y.R.R=R.R.r.r, dans laquelle R est le demi grand axe horizontal et r le demi petit axe vertical.
Ce qui va changer:
- On calcule erreur=X.X.r.r+Y.Y.R.R-r.r.R.R
- Au départ erreur=(R/2).r.r
- Si Y augmente de 1, erreur augmente de (2Y-1).R.R
- Si X diminue de 1, erreur diminue de (2X+1).r.r
- Pour s'arrêter, il faut regarder si le point tracé est bon (si on doit se déplacer deux fois à gauche, c'est fini)
| >4-2) Sens du tracé. |
Pour tracer un cercle, On est parti du point (R,0), avec des Y croissants. Même avec toutes les approximations possibles, on était obligé de se racorder parfaitement grâce aux symétries (la main qui touche le miroir est obligée de toucher son image). Ce n'est plus le cas ici, car on va tracer l'arc 1 et l'arc 2 avec des formules différentes.
Pour raccorder parfaitement, il y a la solution de continuer à tracer dans le sens trigonométrique. Il y aura d'ailleurs un autre avantage: Pour finir, il suffit de tester X=0.
| >4-3) Carrés de R et de r. |
| l | L'algorithme est pour l'instant: pour tracer la première partie
d'un cercle:
|
Que va-t-on améliorer? Les multiplications bien sûr, c'est souvent le point faible. Notons tout d'abord que si on multiplie par k la quantité erreur, cela ne change rien, car on teste si elle est positive ou non. Il y a deux multiplications à faire (Y.R.R n'en fait qu'une, car le terme R.R est une constante qui peut être calculée qu'une fois pour toutes). Comme la multiplication Y.R.R apparait à chaque boucle, c'est elle que l'on va supprimer. Soit k la quantité r.r/R.R . En multipliant erreur par R.R:
| l | Pour tracer la première partie d'un cercle:
|
| l | Il y a deux multiplications |
Alors là, on a bien arrangé la première multiplication, on ne peut pas faire mieux: elle a disaparue. Reste la deuxième qui se calcule environ deux fois moins souvent. Si on approxime k par P/Q (P et Q entiers), au moins l'un des deux étant une puissance de 2, multiplier par k donne une multiplication (ou une division) et un décalage.
| >4-4) Algorithme des ellipses de Martin. |
| l | Pour tracer un cercle:
|
| >4) Tracés en mode 13h. |
La suite de cet article commente l'implantation de l'algorithme de Martin pour tracer des faux et des vrais cercles en mode 13h avec le turbo Pascal 7.0 et en Borland C 2.0 . Il se peut que cet algorithme fonctionne avec d'autres logiciels, et je m'en réjouirais.
| >4-0) Le clipping. |
| l | Et si ça sort de l'écran? |
Dans le tracé de droites, je n'avais pas éprouvé le besoin de vérifier que les points tracés étaient bien dans l'écran. A priori si on donne deux points, on peut faire en sorte qu'ils le soient. A vous sinon d'écrire le code pour couper vos droites. Il n'en est pas de même pour les cercles: le centre déja peut se trouver en dehors de l'écran pour ne faire apparaître qu'un morceau de cercle. J'ai donc choisi ici de ne dessiner que les points dans l'écran. Sans cette précaution, un point situé trop à droite serait dessiné à gauche...
Les points sont dessinés deux par deux par la procédure dpoint. Elle teste si l'ordonnée est dans les limites de l'écran, et si tel est le cas, elle teste si les abscisses le sont aussi. Elle dessine les points qui satisfont les deux tests. Tracer les points deux par deux économise un test d'ordonnée (le quart des tests).
| >4-1) La valeur de k. |
En mode 13h, les pixels sont sensiblement 1,2 fois plus larges que haut. En conséquence le paramètre k vaut 1/(1,2.1,2). Si je prends pour Q le nombre 128, j'obtiens P=89.
On doit prendre pour Q, un nombre suffisament grand pour que P/Q ne soit pas trop faux, mais suffisament petit pour que les calculs puissent encore se faire sur mots de 16 bits (avec des complilateurs 16 bits) pour aller vite. 128 semble une bonne valeur.
| >4-2) Initialisation de l'erreur |
Vrai, on doit mettre -R.k/4. Mais vu les approximations, on peut mettre -R/4. Comme il faut mettre plus petit, j'ai mis -R/2.
| >4-3) Le programme |
Deux versions, l'une en Pascal (LIEN), l'autre en C (LIEN) sont quasi identiques. Vous avez aussi un exécutable (LIEN (celui du pascal car il est 4 fois plus petit). Les sources donnent:
- Le tracé de point avec clipping, qui n'est pas utilisé ici.
- Le sous-programme dpoint qui permet de tracer deux points.
- Le sous-programme cercle qui permet de tracer des cercles dans les modes où les pixels sont carrés.
- Le sous-programme ellipse qui trace des cercles; les paramètres passés sont les coordonnés du centre, le rayon horizontal en pixel, et la couleur. Le rayon vertical est plus petit d'un facteur 1,2.
- Le programme principal définit 3 nombres X, Y et R. (X,Y) sont les coordonnés du centre du cercle que l'on trace, R les rayons. Tout d'abord le programme trace quelques "cercles" puis quelques "ellipses". Ces dernières sont effectivement moins belles que les cercles. Enfin pour faire joli, un serpent de cercles défile. Il fait un tout d'écran chaque 50000 cercles tracés, rien que pour montrer que les tracés d'ellipses sont aussi rapides que les tracés de droites.
| >5) Conclusion |
J'ai montré ce que j'ai trouvé de mieux pour tracer des cercles quelconques d'un point de vue théorique et pratique. N'ayant pas trouvé d'algorithme parfait pour tracer des ellipses, pensez à moi si vous dénichez cette perle.
Un petit mail pour dire "J'ai rien compris", "T'est pas con" ou "Au secours" permet de remplir mon press-book.
Bon courage!