| >Présentation : |
Salut à vous programmeurs, programmeuses. Je m’appelle loubail et c’est mon premier article pour prograzine, un super méga cool zine sur la programmation. (Bon d’accord j’en fait peut-être un peu trop :) ). (NDLR : non, non, tu as tout à fait raison :))
Dans cet article je vais traiter un sujet qui sans nul doute va en interesser plus d’un : les fractales. Pour un premier article j’ai essayé de pas faire trop hard. Mon article va expliquer en quoi consiste une fractale, va donner un petit cours de Maths à ceux qui en ont besoin (!) et enfin attaquer la programmation en vous expliquant (et j’espère que je serai assez clair) comment afficher de belles fractales de l’ensemble Julia sur votre ptit écran.
Si cet article vous a donné envi d’en savoir davantage sur les fractales, de connaître d’autre formules, si vous n’avez rien compris, si vous vous en fichez faites le moi savoir !
Ecrivez moi à loubail@club-internet.fr LIEN ou bailsite@hotmail.com LIEN
Enfin n’hésitez pas à venir visiter mon site :
Site en français : http://www.multimania.com/loubail/ LIEN
Site en anglais : LIEN
P.S. : Si j’élabore un nouvel article sur les fractales j’incorporerai probablement des liens vers des sites consacrés aux fractales. Si les fractales vous passionnent mailez moi des adresses de sites consacrés aux fractales. Comme ça tout le monde en profitera ( et moi en premier !).
| >Fractale et géométrie fractale : |
En 1958 Benoît Mandelbrot rejoint IBM, où il commença une analyse mathématique des bruits en électronique et commença à percevoir une structure dans laquelle une série de fluctuations de toutes tailles ne pouvaient pas être expliquée par les méthodes statistiques existantes.
Chaque fois qu’il résolvait un problème un autre du même type que le précédant mais à une échelle plus petite apparaissait. Il appela alors ceci la géométrie fractale.
Le terme fractal vient du latin frangere brisé et fractus irrégulier morcelé. C’est une figure géométrique irrégulière voire fragmentée quelle que soit l’échelle qui détient une borne supérieure et une borne inférieure. Elle possède des éléments spécifiques et ses parties ont la même structure que le tout.
La géométrie fractale est donc l’étude d’objets qui à toutes les échelles possèdent les mêmes caractéristiques.
Afin de mieux cerner la nature d’une fractale voici la représentation à l’aide d’un ordinateur de la fractale MANDELBROT .
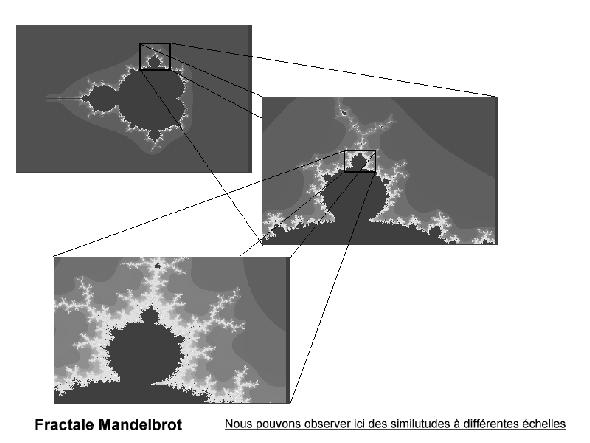
Cette nouvelle géométrie se base sur un principe très important : le principe d’échelle. En effet un objet fractal comme nous venons de le voir précédemment possède la même structure à différentes échelles, à différents grossissements. De ce fait lorsqu’on agrandit un objet fractal les détails sans importance changent et prennent une autre valeur. Ceci permet d’affirmer que chaque partie d’une fractale est importante et représente l’information révélant la construction de la fractale. ( Le document ci-dessus nous fait part de cette étonnante propriété).
Une fractale est un objet invariant à toute échelle qui permet de décrire des formes rencontrées dans la nature comme les nuages, les arbres, les côtes de Bretagne (Ces phénomènes qui n’ont rien en commun partagent alors la même structure mathématique).

Les objets fractales sont ainsi à l’origine d’une nouvelle géométrie décrivant mieux la nature que ne le faisait la géométrie traditionnelle.
Le calcul des fractals s’applique aux transmissions téléphoniques, à l’astronomie, à la météorologie, à l’hydrographie, à la médecine. Leur domaine fut d’abord celui des turbulences (fusée, avion, automobile) et fut illustré par la carte des côtes de Bretagne.
Afin de pouvoir modéliser, à l’aide de formules mathématiques, ce type d’objet, la géométrie fractale doit pouvoir parfaitement les décrire.
Pourtant la géométrie fractale se base sur des modèles statistiques. Ceci peut donc surprendre car nul ne peut tenir compte du hasard pour décrire parfaitement un objet ou un fait.
| >Un peu de Mathématiques : |
Bon avant d’expliquer quel type de procédé mathématique vous devez utiliser pour obtenir une fractale sur votre écran il me faut tout d’abord présenter ( à ceux qui ne le savent pas) , succintement, l’ensemble de nombre dans lequel ce procédé prend place : l’ensemble des complexes noté : " .
| >Ensemble C : |
Bon ben là pour être suffisamment clair je sors mon cours de Maths de Terminal et je recopie :
Définitions et notations :
- On admet l’existence d’un nombre imaginaire, noté i, vérifiant i² = -1.
- Un nombre complexe est un nombre de la forme x + iy, où x et y sont deux nombres réels.
- L’ensemble des nombres complexes est noté C (NDLR: en fait, c'est un C avec une barre à l'intérieur, mais c'est pas évident de trouver ce signe avec la police par défaut !!) .
| >Théorème : |
Tout nombre complexe z admet une écriture unique de la forme x + iy, où x et y sont des réels.
Cette écriture est la forme algébrique de z où :
x est la partie réelle de z, notée Re(z) ;
y est la partie imaginaire de z, notée Im(z) .
| l |
Autre définition : Pour tout nombre complexe z de fomr algébrique x + i y, le module de z est le nombre réel positif : ?(x² + y²), noté |z| (NDLR: et lu "module de z")
On en déduit que |z|² = x² + y².
Bon ben on fait quoi avec ça ? Et ben on fait des calculs J
| >Calculs dans C |
Soit z et z’ deux nombres complexes :
On a z = x + iy et z’ = x’ + iy’
z + z’ = ( x + x’ ) + i ( y + y’ )
z z’ = ( x x’ – y y’ ) + i ( x y’ + x’ y )
Bon je n’irais pas plus loin dans les explications car vous n’avez pas besoin de connaître d’autre choses pour obtenir un rendu d’une fractale Julia !
| >Suites complexes : |
Les fractales possèdent 3 propriétés importantes :
- 1°) Elles sont générées par des calculs relativement simples répétés encore et encore jusqu’à atteindre une certaine valeur (Ce que les ordinateurs font très rapidement).
- 2°) Elles sont, littéralement, infiniment complexes : elles révèlent de plus en plus de détails sans limite lorsqu’on dessine des aires de plus en plus petites.
- 3°) Leurs représentations peuvent être étonnamment belles lorsqu’on les modélise à l’aide d’ordinateur.
Dans cet article je ne m’intéresserais qu’aux fractales dont le calcul mathématique est assez simple et que l’on représente en 2 dimensions. Je ne ferai pas référence aux fractales utilisant l’algèbre hypercomplexe. ( et oui ça existe J J J ).
Soit P(z) une fonction répétée successivement pour générer une fractale.
Par exemple pour une fractale du type Julia P(Z)=Z² + C (avec Z et C E C) (NDLR: Z et c appartiennent à C - ensemble des complexes)
Soit PK(Z) le résultat de l’itération de la fonction P pour K itérations. On peut tout aussi bien utiliser la notation PKC(Z) si la fonction P possède un paramètre C (ce que je vais considérer dans l’exemple suivant).
Soit A(C) = inf{ |PKC(0)|,K=1,2,3,...}
Soit E l'ensemble des modules des images de 0 par PKC. On a card(E)=K c'est-à-dire que E contient K éléments. A(C) est alors la valeur la plus proche de 0 appartenant à E. (car un module est toujours positif)
On attribue alors à C la valeur du K associé à inf{ |PKC(0)|,K=1,2,3,...} c'est à dire la valeur de K avec laquelle on obtient la valeur la plus proche de 0 appartenant à E.
Lorsqu’on représente une fractale on accorde une couleur à chaque point associé à la longueur de ce cycle. En gros on répète un même calcul n fois jusqu’à dépasser une certaine valeur. (ce calcul est tout simplement la suite).
Par exemple les points qui approchent un point fixé auront la couleur 1. Les points qui approchent 2 cycles ont la couleur 2. Les points qui n’approchent pas un cycle durant l’itération ont la couleur maximale pouvant être assignée. Ceci marche bien avec un nombre relativement important d’itération.
J’en vois déjà qui s’affole. Ne craignez rien ce n’est pas très complexe. ( fallait bien que je le place quelque part )
Vous allez tout de suite mieux comprendre : ( c’est ce qu’on dit toujours ;) )
Les fractales de l’ensemble julia sont des fractales qui se basent sur la suite complexe
Z(n+1) = Z(n)² + C | l |
(Je vous montre tout d’abord un rendu de cette fractale )
Celle qui suit a été calculée avec le paramètre suivant : C(0) = 0.3 + 0.6 i

N’est – elle pas magnifique ? Et encore elle n’est quand noir et blanc !
Z(n+1) = Z(n)² + C | l |
On assigne une valeur qui restera fixe à C : par exemple C(0) = 0.3 + 0.6 i
Comme on utilise une suite récurrente on assigne ensuite à Z(0) les coordonnées d’un point donné dans le plan.
Puis on initialise une boucle dans laquelle on modifie la valeur de z comme suit : z = z² + C jusqu’à ce que |z|² (c’est – à – dire x² + y² ) dépasse une certaine valeur (560 par exemple).
Quand la boucle est terminée ou si la boucle a été exécuté n fois ( par exemple s’il y a eu 200 cycles) on recommence ce processus avec un autre point.
Avec cette méthode on balaye un certain nombre de points dont les coordonnées sont comprises entre (-2 , -2 ) et ( 2, 2 ). ( Et oui on ne trouve des julias seulement dans ce secteur ).
Bon maintenant que vous avez tout compris et que je vous ai filé le processus à suivre on va pouvoir passer à la partie tant attendue, la partie programmation.
| >Programmation : |
Pour ce programme et je vais décomposer z en x + iy et donc élaborer 2 suites :
X(n+1) = X(n)²-Y(n)² + Re( C ) Y(n+1) = 2*X(n)*Y(n) + Im( C ) | l |
| >Comment j’ai fait ! |
C’est plutôt simple. Soit z un nombre complexe.
On pose z=x + iy et C = Cx + Cy i
Z² + C = (x + iy)² = x² - y² + Cx + i ( 2 x * y + Cy ) (Cf petit cours de Mathématiques)
Ainsi Re(Z² + C) = x² - y² + Cx et Im(Z² + C) = 2 x*y + Cy
Voilà, maintenant vous avez compris !
| l | N.B.: Bien que ce programme est élaboré en C il sera facile de porter ce programme dans un autre langage. |
Je tiens compte du fait que vous avez des notions de programmation graphique et de programmation en c. Si vous n’en avez pas jetez un œil sur les articles des précédents numéros de prograzine. D’abord je place des fichiers en-têtes :
#include <conio.h>
#include <dos.h>
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <complex.h>
//Fonction Principale
void main(void)
{
// *screen est un pointeur qui pointera vers la mémoire écran
unsigned char far *screen;
float x,y;
//On pose C = Cx + i*Cy
float Cx=0.3;
float Cy=0.6;
int num;
long tab=0;
complex z,c,z2;
float x2,y2,x4,y4;
int a;
union REGS regs;
//On initialise le mode vidéo VGA 320*200 256 couleurs
regs.x.ax=0x0013;
int86(0x10,®s,®s);
//J'aurai très bien pu utiliser :
//asm{ mov ax,13h
// int 10h
// }
//On fait en sorte que screen pointe vers la mémoire vidéo VGA
screen = (unsigned char far *) MK_FP(0xA000, 0);
// c=complex(Cx,Cy);
//On met en place deux boucles : avec x et y on assignera à Z(0) x + i*y
for(y=-2;y<=2;y+=0.02)
{
for(x=-2;x<=2;x+=0.0125)
{
// z=complex(x,y);
x4=x;
y4=y;
num=0;
x2=0;
y2=0;
//Maintenant on met en place la boucle associée à la suite Z(n+1)=Z(n)²+C
// num contiendra le nombre de cycles effectuées dans la boucle suivante
// a est un indicateur : si a=0 alors la boucle peut continuer
// si a=1 alors on a dépasser sans problème la valeur //fixée. On arrête alors la boucle.
// si a=2 alors on arrive pas à dépasser la valeur //fixée. On arrête alors la boucle.
// num=0;
for(num=0;a==0;num++)
{
//Si on dépasse un certain nombre de cycles on assigne à a la valeur 2
if(num>=200) a=2;
if((x2*x2+y2*y2)>=560) a=1;
/* if(num>=200) a=2; //si on a dépassé 200 cycles a=2
if((x2*x2+y2*y2)>=560) a=1; //si |z|²>=576 a=1*/
// z2=z*z+c;
// z=z2;
x2=x4*x4-y4*y4+.3;
y2=2*x4*y4+.6;
x4=x2;
y4=y2;
//Si on appuie sur une touche arrête le programme ( très pratique
//si le //programme plante ou si le calcul est trop long !
/* if(kbhit())
{
regs.x.ax=0x0003;
int86(0x10,®s,®s);
exit(1);
}*/
}
screen[tab]=num+20;
if(a==2) screen[tab]=0;
tab++;
}
}
getch();
regs.x.ax=0x0003;
int86(0x10,®s,®s);
}
| l |
Bon ben c’est terminé pour cette fois-ci. J’espère avoir interesser un maximum de personnes et recevoir des tonnes de mail, de questions, etc… (pas trop quand même).
P.S. : Ne vous amusez pas à faire du copier-coller : utiliser le fichier Julia.c fourni LIEN