Salut a tous, dans ce second article sur les fractales j’ai decide de vous presenter la fractale Newton d’une maniere differente que la fractale Julia. En effet je vais non seulement vous expliquer la methode permettant de l’afficher mais aussi essayer (Je dis bien essayer) de vous expliquer son allure! ;)
Avant de partir dans le monde des fractales il faut tout d’abord comprendre comment fonctionne la methode de Newton (ou plutot la methode des tangentes) ;).
| >I\ La methode Newton : |
Soit f une fonction polynome definie sur un intervalle tel que sur cet intervalle f(x)=0 . Avant de commencer a parler de la methode Newton il faut demontrer l’existence et l’unicite de ¥ solution de f(x)=0 sur l’intervalle choisi.
| >Existence et unicite de la solution de f(x)=0: |
Avant de commencer a demontrer l’unicite de ¥ je vais faire des considerations :
- Sur l’intervalle [a ;b] f est derivable
- Sur l’intervalle [a ;b] f est strictement croissante ou strictement decroissante.
- Il faut que 0 appartienne a l’intervalle image de [a ;b] par f (On admet alors l’existence de ¥)
- Il faut que [a ;¥] soit stable par g, g etant defini par g(x)= x – f(x)/f ’(x)
- Enfin il faut que g(a) appartienne a [ k;¥] avec k tel que g’(k) = a
f est deux fois derivable sur [a ;b]
f est soit strictement croissante soit strictement decroissante sur [a ;b]
Si f est croissante alors f est une bijection de [a ;b] vers [f(a) ;f(b)]
Si f est decroissante alors f est une bijection de [a ;b] vers [f(b) ;f(a)]
0 appartient a l’intervalle image de [a ;b] par f.
Ainsi l’equation f(x)=0 admet une seule solution ¥ qui appartient a l’intervalle [a ;b]. Evidemment selon l’equation de f on peut reduire l’intervalle [a ;b] afin d’obtenir un encadrement plus petit de ¥.
| >Methode de Newton : |
Nous venons de demontrer l’existence et l’unicite de ¥. Desormais nous allons etudier une methode permettant de determiner une valeur approchee ¥. : la methode de Newton ;)
- ¥ appartient a l’intervalle [a ;b]
On pose U0=a. Et on remplace la fonction f par la fonction affine dont la representation graphique est la tangente T1 a la courbe representative de f au point A(a ;f(a))
- f est derivable sur [a ;b]
L’equation de T1 est donc : f ‘ (a) (x – a) + f (a)
- On pose U1 le point d’intersection de T1 et l’axe des abscisses.
Le point U1 est ainsi solution de f ’ (x) (x – a) + f (a)
f ‘ (a) (x – a) +f (a) = 0 ó f ’ (a) (x – a) = - f (a) <=> f ’ (U0) (x – U0) = -f (U0) <=> x = U0 – f (U0) / f ‘ (U0) | l |
Donc U1 = U0 – f(U0) / f ‘ (U0)
Pour tout entier naturel n superieur ou egal a 0 on resout l’equation f ‘ (Un) (x – Un) + f (Un) = 0 ( C’est l’equation de la tangente a la courbe representative de f en Un)
On pose que Un+1 est solution de cette equation Donc f ‘ (Un) (x – Un) + f (Un) = 0 <=> Un+1 = Un – f (Un) / f ‘ (Un)
On obtient alors une suite interessante a etudier. ;)
| >Etude de la suite Un+1 = Un – f(Un) / f ’ (Un) |
Soit g la fonction definie sur [a;b] par g(x) = x – f (x) / f ‘ (x)
Nous allons etudier les variations de g. Donc on va tout d’abord etudier le signe de g’
Comme f est strictement decroissante ou strictement croissante sur [a;b] f ’ (x) est different de 0 pour tout x appartenant a [a;b].
f est deux fois derivable sur [a ;b] donc f ‘ est derivable sur [a ;b]
ainsi f ‘ est derivable et non nulle sur [a ;b]
f est derivable est derivable sur [a ;b]
x -> x est derivable sur [a ;b] comme fonction de reference
Donc par quotient puis par somme g est derivable sur [a ;b]
Pour tout x appartenant a [a ;b] g ‘ (x) = 1 – ( f ‘ (x) . f ‘ (x) – f(x) . f ‘’ (x) ) / (f ‘ (x) )²
= f(x) . f ‘’ (x) / ( f(x) )²
L’intervalle d’etude qui nous interesse est [a ;¥]
- si sur [a ;¥] f est strictement croissante alors sur [a ;¥] f ‘ , qui represente le coefficient de la tangente a la courbe representative en x , est strictement croissante. Comme sur [a ;¥] f ‘ est strictement croissante on a pour x appartenant a [a ;¥] f ‘’ (x) positif.
- si f est strictement croissante sur [a ;b] et si f(¥) = 0 alors sur [a ;¥] f(x) >= 0
ansi sur [a ;¥] f(x) et f ‘’ (x) sont positifs. Comm ( f ‘ (x) )² >= 0 alors g’(x)>=0
- si sur [a ;¥] f est strictement decroissante alors sur [a ;¥] f ‘ , qui represente le coefficient de la tangente a la courbe representative en x , est strictement decroissante. Comme sur [a ;¥] f ‘ est strictement decroissante on a pour x appartenant a [a ;¥] f ‘’ (x) negatif.
- si f est strictement decroissante sur [a ;b] et si f(¥) = 0 alors sur [a ;¥] f(x) <= 0
ansi sur [a ;¥] f(x) et f ‘’ (x) sont negatifs. Comme ( f ‘ (x) )² >= 0 alors g’(x)>=0
Donc quelquesoit la variation de f su l’intervalle considere (strictement croissante ou strictement decroissante) g’ (x) >=0 et g est croissante.
Soit k un reel tel que g’(k) = a
Si k existe alors k appartient a [a ;¥] comme g ‘ est defini sur [a ;¥] (J’ai change l’ensemble de definition de g’ car j’ai changeant de domaine d’etude )
[a ;¥] est stable par g donc pour tout x appartenant a [a ;¥] g ‘ (k) appartient a [a ;¥]
Comme [a ;¥] est stable par g et que k appartient a [a ;¥], [k,¥] est stable par g.
Donc si x appartient a [k ;¥] alors g(x) appartient a [k ;¥]
Sur [a ;¥] g ‘ (x) >=0 et est croissante comme g.
Donc sur [k ;¥] 0<=g ’ (x)<= a
On definit la suite Vn par :
V0 = a et pour tout entier naturel n Vn+1 = g(Vn)
V0 appartient a [a ;¥] donc g(V0) appartient a [a ;¥] comme [a ;¥] est stable par g
Or g(V0) = V1 et g(a),donc g(V0), appartient a [k ;¥] donc V1 appartient a [k ;¥].
V1 appartient a [k ;¥] donc g(V1) appartient a [k ;¥]. Or g(V1)=V2. Donc V2 appartient a [k ;¥].
On pose pour tout n >=1 Vn appartient a [k ;¥]
[k ;¥] est stable par g donc g(Vn) appartient a [k ;¥]. Or Vn+1=g(Vn). Donc Vn+1 appartient a [k ;¥].
Ceci est vrai en n=1 et donc hereditaire pour tout n appartenant a N \ {0,1}
Pour tout n appartenant a N \ {0,1} on a Vn appartient a [k ;¥]
Pour tout x appartenant a [k ;¥] on a 0<= g ‘ (x) <= a
¥ appartient a [k ;¥]
Donc par application de l’inegalite des accroissements finis on a :
| g(Vn) – g(¥) | <= a | Vn - ¥ |
g (¥) = ¥ - f(¥) / f ‘ (¥)
Or f(¥) = 0 donc g (¥) = ¥
De plus g(Vn) = Vn+1
Donc on a : | Vn+1 – ¥ | <= a | Vn - ¥ |
Par une recurrence que je ne tiens pas a vous demontrer, ;) , on a :
| Vn - ¥ | <= a^(n-1) | V1 - ¥ | ( on a n-1 inequations dont chaque membre est positif. On realise un produit membre a membre entre les n-1 inequations ! )
Desormais 4 cas se presentent :
- Soit V1 = ¥ et on a alors la valeur exacte de ¥
- Soit |a| < 1 et donc la limite de a^(n-1) quand n tend vers plus l’infini est egale a 0. Ansi la limite de Vn quand n tend vers plus l’infini est ¥. Donc Vn est une approximation d’autant plus meilleure de ¥ que n est grand.
- Si |a| =1 alors on peut dire que l’erreur d’approximation est toujours la meme pour n appartenant a N \ {0,1}
- Si |a| >1 alors la limite de a^(n-1) quand n tend vers plus l’infini est egale a + ou – l’infini. Si V1 est different de ¥ alors la limite de Vn quand n tend vers plus l’infini est l’infini. Donc Vn est une approximation d’autant plus mauvaise de ¥ que n est grand.
Voilà j’espere que je ne vous aurai pas trop " pris la tete " avec ces mathematiques. ;) Mais ne vous inquietez pas je vais, apres vous avoir presenter la fractale Newton, revenir aux mathematiques ;)
| >II\ La Fractale Newton : |
| >a) Formule permettant de rendre cette fractale : |
Ah enfin, apres tout ce blabla mathematique, ;), je vais vous presenter cette magnifique fractale. Tout d’abord je vous en met une representation.

Et maintenant je vais vous expliquer la methode utilisee pour obtenir ce rendu ;)
Cette fractale est basee comme vous pouvez vous en douter sur la methode de Newton decrite dans la premiere partie de cet article. Au debut de cet article j’ai decrit la methode de Newton appliquee au reel mais on peut tout aussi bien applique cette methode aux nombres complexes ;) La fractale Newton utilise ainsi la methode de Newton appliquee aux complexes avec f(z) = z^p –1 et p appartient a N \ {0,1} La couleur de chaque point est associee au nombre de cycle qui permette d’atteindre une racine de f. On doit ainsi utiliser la suite Zn suivante :
Z(0) = coordonnees d’un point dans le plan complexe considere
Z(n+1) = Z(n) – f (n) / f ‘ (n)
= Z(n) – ( Z(n)^p –1 ) / ( p . (Z(n) ^ (p –1)) )
= ( Z(n).( p . (Z(n) ^ (p –1)) ) – ( Z(n)^p –1 ) ) / ( p . (Z(n) ^ (p –1)) )
= ((p-1).Z(n)^p + 1)/(p.Z(n)^(p - 1))
Donc comme je l’ai precise au debut de l’article je vais tout d’abord essaye de vous expliquer pour quelles raisons cette fractale a cette allure. ;)
| >b) Aspect chaotique : |
Comme je ne detient pas des connaissances mathematiques assez poussees, pour le moment ;), je ne vais pas pouvoir rentrer trop dans les details ! :(
Lorsque vous utilisez l’algorithme de Newton vous essayer de trouver les racines d’une fonction polynome par des tatonnements qui convergent vers les racines comme vous incorporez dans la formule developpee par Newton les resultats de chaque approximation (Cf etude de la suite dans I). Cet algorithme est tres pratique. Neanmoins si vous prenez une valeur qui se situe entre deux racines il y aura un probleme ! Dans ce cas, il y aura une divergence qui s’effectuera de plus en plus rapidement au fur et a mesure des iterations. ( Cf les 4 cas dans l’etude de la suite dans I). Cette divergence est alors a l’origine d’un chaos ! ;)
| >c)Allure de la fractale : |
Avant de passer de passer au cas general je vais m’interesser a la representation de la fractale Newton representee dans cette article ! La fractale Newton representee est associee a l’equation f(z) = z^3 -1 Comme vous pouvez le constater l’aspect chaotique decrite ci-dessus prend place.
On distingue 3 branches, ou plutot rayons, autour desquelles de mysterieuses choses s’entremelent. Dans cette article je ne vais pas vous expliquer ce que sont ces mysterieuses choses, leur nature, etc… Je vais plutot m’interesse aux branches et expliquer des raisons qui determinent leur position. ;) ( C’est deja beaucoup ;) ) Pour demontrer leur existence je ne vais pas utiliser le cas particulier qui utilise p=3. :(
Soit p un entier naturel strictement superieur a 1.
f est telle que f(z) = z^p – 1
La methode de Newton nous permet d’obtenir une approximation des racines de f.
f(z) = 0 <=> z^p –1 = 0
<=> z^p = 1
Or l’equation z^p = 1 donne les racines p ieme de l’unite! ;) Nous allons donc pouvoir placer les racines de f dans un repere orthonormal direct (0 ; i ; j ) (je ne mets pas la syntaxe des vecteurs parce que tout le monde n’a peut etre pas la police d’ecriture adequate :( )
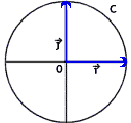
L’equation z^p = 1 dispose de p racines notees A0 … A(P-1). Chaque racine se situent sur le cercle C. Ces racines forment un polynome regulier A0….A(P-1) de centre 0 tel que 0A0 = 1
Soit k un entier tel que 0<=k<=p Soit ak les affixes des points Ak
On a ak = e^(i*(2.PI / p)*k
Donc arg(ak) = k*2.PI/p (mod 2.PI)
Ainsi on obtient l’angle (i , 0Ak). On peut alors placer les racines p ieme de l’unite sur C.
En revenant au cas particulier avec p=3
On a : arg(a0) = 0, arg(a1) = 2.PI/3, arg(a2) = 4.PI/3 = -2.PI/3 (et tout ca modulo 2.PI)
On obtient alors la figure suivante :
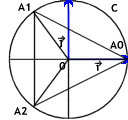
Desormais je vais supperposee la fractale Newton calculee avec p=3 avec la figure representee ci-dessus.
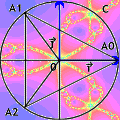
Les trois branches, danslesquelles un chaos prend place, se situent a la meme distance des deux droites avoisinnantes qui relient le centre du repere complexe aux racines cubique de l’unite ! (Cf. Aspect chaotique).
Enfin on peut noter que de nombreuses symetries prennent place !
Voilà je pense avoir termine de vous parler des choses simples concernant cette fractale. Je vais desormais passer au stade de la programmation.
Avant de commencer a vous parler de programmation je voudrais demander aux lecteurs qui sont en mesure d’etudier plus precisement la fractale Newton de me contacter a loubail@club-internet.fr ou a bailsite@hotmail.com ou meme d’ecrire un article pour Prograzine ;)
| >III\ Programmation : |
| >a)Algorithme : |
L’algorithme n’est pas compliqué :
On pose z l’affixe d’un point dans le plan complexe considere. On attribue a ce point une couleur associe au nombre d’iteration effectuee. Dans une iteration on effectue les operations suivantes : z=((p-1)*pow(z,p)+1)/(p*pow(z,p-1)); x4=real(z) ; y4=imag(z) ; si |1-(x4*x4+y4*y4)|< 0.0000001 on arrete les iterations et on passe au point suivant ! | l |
Une fois la fractale affichee vous constaterez quelques differences avec les representations de fractales Newton que vous auriez deja vu ! Ceci est du a la valeur 0.0000001 qui n’est pas assez petite ! Donc ne vous inquietez pas !
Enfin je tiens a signaler que j’ai employe le type complex d’une part parce que la decomposition de la suite complexe n’est pas agreable (surtout si on a un p important !) et d’autre part car vous pourrez afficher la fractale Newton pour n’importequel p >=2 !
| >c)Fichier : |
Bon ben la je vais copier coller mon fichier source ;) :
//Newton.cpp by Loubail loubail@club-internet.fr
// bailsite@hotmail.com http://www.multimania.com/loubail
// http://www.geocities.com/SiliconValley/Chip/8195
//Les fichiers en-tete
#include <conio.h>
#include <dos.h>
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <complex.h>
//La fonction principale
void main(void)
{
unsigned char far *screen; //screen pointera vers 0xA000
//variables diverses
char num;
float x,y,x2,y2,x4,y4,minx,maxx,miny,maxy,stepx,stepy;
float x5,y5;
float qx=-1.5;
float qy=1.4;
float temp;
int h,j;
int tab=0;
union REGS regs;
complex z,z2;
int a,p;
//on va utiliser la methode de Newton appliquee sur z^3 –1 = 0 ;)
p=3;
//On initialise le mode VGA !
regs.x.ax=0x0013;
int86(0x10,®s,®s);
//screen va pointer vers 0xA000
screen = (unsigned char far *) MK_FP(0xA000, 0);
for(y=-2;y<=2;y+=0.02) // 4 /200
{
for(x=-2;x<=2;x+=0.0125) // 4 /320
{
x4=x;
y4=y;
num=0;
x2=0;
y2=0;
a=0;
for(num=0;a!=1;num++)
{
if((x4*x4+y4*y4)<=1.0000001) if((x4*x4+y4*y4)>=0.9999999) a=1;
//on arrete si on appuie sur une touche !
if(kbhit())
{
regs.x.ax=0x0003;
int86(0x10,®s,®s);
exit(1);
}
//on applique l’algorithme
z=complex(x4,y4);
z=((p-1)*pow(z,p)+1)/(p*pow(z,p-1));
x4=real(z);
y4=imag(z);
}
//on affiche le point
screen[tab]=num+20;
tab++;
}
}
//On attend que l’utilisateur appuie sur une touche
getch();
//On restaure le mode TXT !
regs.x.ax=0x0003;
int86(0x10,®s,®s) ;
}
| l |
| >IV\ Conclusion : |
N’ayant recu aucun courier de lecteurs me specifiant des adresses de sites consacres aux fractales je ne peux pas vous mettre les adresses de tels sites ! :(
Si vous etes interesses par les fractales faites le moi savoir ! On pourrait corediger des articles ! :) :)
J’espere avoir ete suffisamment clair. Si vous voulez me poser des questions, si vous avez des remarques, si vous voulez me donner votre avis sur cet article ecrivez-moi a : loubail@club-internet.fr ou bailsite@hotmail.com
Vous pouvez aussi visiter mon site : http://www.multimania.com/loubail/ (Site en francais) ou http://www.geocities.com/SiliconValley/Chip/8195 (Site en anglais).