Régression non linéaire Théorie Position du problème Principe de la méthode de Marquardt L'algorithme de Newton-Raphson L'algorithme de Marquardt Qualité de l'ajustement Coefficients de détermination Variance expliquée, variance résiduelle Précision des paramètres Programmation en Turbo Pascal Présentation générale Description des fonctions et procédures Adaptations possibles Changement des fonctions de régression ou de variance Changement de l'algorithme de minimisation Exemples Concentration d'un médicament en fonction du temps Activité d'une enzyme en fonction de la concentration du substrat   I. Théorie I.A. Position du problème On cherche à exprimer la relation entre deux variables x et y sous forme d'une fonction f qui dépend de manière non linéaire d'un vecteur de paramètres B : Soit par exemple une fonction exponentielle (Fig. 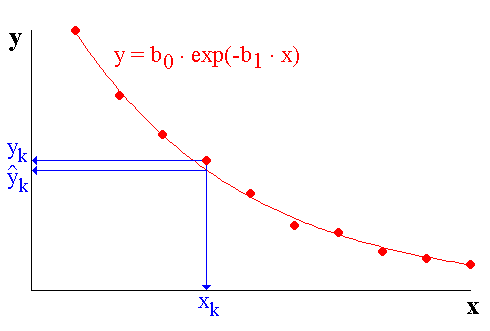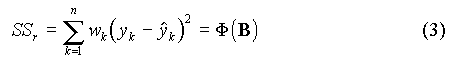1) : Figure 1 : Régression non linéaire (Exemple : fonction exponentielle) Comme pour la régression linéaire, nous allons chercher les valeurs des paramètres B qui rendent minimale la somme des carrés des écarts pondérée : Lorsque f est une fonction non linéaire des paramètres B, le minimum ne peut être trouvé que par une méthode itérative : on part avec une estimation initiale des paramètres, que l'on affine à chaque étape jusqu'à ce que les paramètres ne varient plus. Parmi les nombreux algorithmes de minimisation disponibles, nous étudierons essentiellement la méthode de Marquardt, qui est l'une des plus utilisées en régression non linéaire. I.B. Principe de la méthode de Marquardt L'algorithme de Marquardt est en fait une amélioration d'un algorithme plus classique, celui de Newton-Raphson. I.B.1. 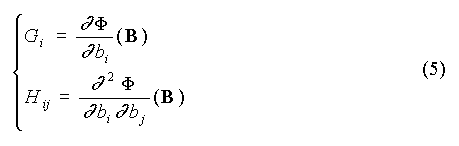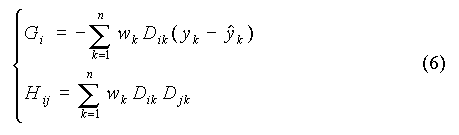L'algorithme de Newton-Raphson Si B désigne le vecteur des paramètres estimé à l'itération courante, une meilleure estimation B' est donnée par la formule : où G désigne le vecteur gradient de la fonction à minimiser, et H la matrice hessienne, ou matrice des dérivées secondes : Pour la régression non linéaire, on utilise les approximations suivantes de G et H : où Dik désigne la dérivée de la fonction de régression par rapport au paramètre bi, évaluée au point xk. Remarques : La transposée de la matrice D ainsi définie est la matrice jacobienne J = DT Les formules (6) équivalent à diviser G et H par 2 et à négliger dans l'expression de Hij le terme contenant ek2, avec : En effet ce terme tend vers zéro à mesure que les itérations progressent et que la valeur calculée de y se rapproche de la valeur observée. I.B.2. L'algorithme de Marquardt En vue d'améliorer la convergence de l'algorithme de Newton-Raphson, Marquardt (J. Soc. Indust. Appl. 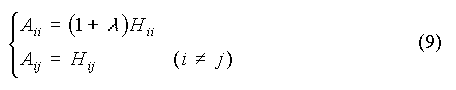Math., 1963, 11, 431-441) remplace la matrice hessienne H par la matrice A définie par : 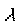est un scalaire initialisé (p. ex. à 1) au début des itérations, puis divisé par 10 si l'itération est efficace (c'est-à-dire si SSr diminue) ou sinon multiplié par 10. La valeur de 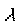diminue ainsi à mesure que SSr tend vers son minimum. Une fois le minimum atteint, on fait une dernière itération avec 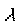= 0 pour pouvoir calculer H-1 (qui servira à estimer la matrice de variance-covariance des paramètres). I.C. Qualité de l'ajustement I.C.1. 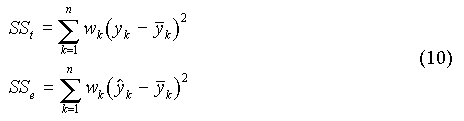Coefficients de détermination Par analogie avec la régression linéaire, on définit : Le coefficient de détermination : r2 = SSe / SSr Le coefficient de détermination ajusté : r2a = 1 - (1 - r2) &middot; (n - 1) / (n - p) où p désigne le nombre de paramètres du modèle, et : Mais si le modèle s'ajuste mal aux données, ou si le minimum est mal localisé, on peut avoir SSe > SSt et donc r2 > 1. Dans ce cas le coefficient de détermination n'est pas exploitable. C'est le signe d'un mauvais ajustement. 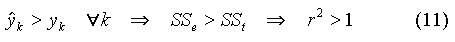Par exemple, si la courbe calculée passe toujours au-dessus des points, on a : I.C.2. Variance expliquée, variance résiduelle Comme pour la régression linéaire, on définit : La variance expliquée par : Ve = SSe / (p - 1) La variance résiduelle par : Vr = SSr / (n - p) Sous l'hypothèse de normalité des résidus, le rapport F = Ve / Vr suit approximativement une loi de Snedecor à (p - 1) et (n - p) degrés de liberté. Ces critères sont utiles pour comparer différents modèles. Pour une fonction de variance donnée, le meilleur modèle est celui qui correspond à la plus faible valeur de Vr et aux plus fortes valeurs de r2a et F. I.C.3. Précision des paramètres La matrice de variance-covariance des paramètre est estimée par V = Vr . H-1, où H est la matrice hessienne, définie en I.B.1. On en déduit les écart-types des paramètres : si = (Vii)&frac12; Sous l'hypothèse de normalité des résidus, les paramètres suivent approximativement une loi de Student à (n - p) degrés de liberté. On peut donc comparer chaque paramètre à zéro au moyen du rapport : ti = bi / si. II. Programmation en Turbo Pascal La programmation des calculs précédents peut être réalisée au moyen de la bibliothèque TP MATH. II.A. Présentation générale Les programmes suivants sont disponibles dans TPMATH2.ZIP : FITEXPO.PAS pour l'ajustement d'une somme d'exponentielles (jusqu'à 3 exponentielles) : 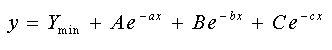FITFRAC.PAS pour l'ajustement d'une fraction rationnelle : 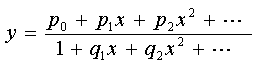Ces programmes utilisent des procédures situées dans 4 fichiers à inclure : REG_IN.INC pour la lecture des données dans le fichier d'entrée REG_NL.INC pour les calculs de régression non linéaire REG_OUT.INC pour l'écriture des résultats dans le fichier de sortie REG_PLOT.INC pour le tracé des points et de la courbe calculée II.B. Description des fonctions et procédures Les principales fonctions et procédures définies dans ces programmes sont les suivantes : function VarFunc(Y : Float) : Float; Cette fonction, notée g(y), est utilisée par la régression pondérée, pour calculer la variance d'une observation y (cf la régression linéaire pondérée). La vraie variance est égale à Vr.g(y), où Vr est la variance résiduelle, qui sera estimée par le programme. Exemple avec g(y) = y2 : function VarFunc(Y : Float) : Float; begin VarFunc := Sqr(Y); end; Remarque : La régression non pondérée correspondrait à VarFunc := 1 procedure ReadCmdLine; Cette procédure lit les paramètres passés sur la ligne de commande. Ces paramètres sont : Le nom du fichier d'entrée (extension .DAT par défaut). Le nombre d'exponentielles (pour FITEXPO), ou bien les degrés du numérateur et du dénominateur (pour FITFRAC). Tous ces paramètres ont par défaut des valeurs égales à 1. Un paramètre valant 1 si la fonction inclut un terme constant (Ymin ou p0) .   function FuncName : String; Cette fonction retourne le nom de la fonction à ajuster (p.ex. 'y = A.exp(-a.x)'). function FirstParam : Integer; Cette fonction retourne l'indice du premier paramètre ajusté. function LastParam : Integer; Cette fonction retourne l'indice du dernier paramètre ajusté. function ParamName(I : Integer) : String; Cette fonction retourne le nom du Ième paramètre. RegFunc(X : Float; B : PVector) : Float; C'est la fonction de régression. B est le vecteur des paramètres. procedure DerivProc(X : Float; B, D : PVector); Cette procédure calcule les dérivées partielles de la fonction de régression par rapport aux paramètres. En sortie, D^[I] contient la dérivée par rapport au paramètre B^[I]. Les deux exemples fournis utilisent l'expression analytique des dérivées. Cette méthode est recommandée car elle est la plus précise et souvent la plus rapide (dans la mesure où les dérivées ont des expressions simples !). Dans le cas général, on peut utiliser une procédure de dérivation numérique telle que la suivante : procedure DerivProc(X : Float; B, D : PVector); var I : Integer; Eps, Temp, Y, Y1 : Float; begin { MACHEP est une constante définie dans FMATH.PAS et qui représente la précision des nombres à virgule flottante (fonction du type utilisé) } Eps := Sqrt(MACHEP); Y := RegFunc(X, B); for I := FirstParam to LastParam do begin Temp := B^[I]; { Sauver paramètre } B^[I] := B^[I] + Eps * Abs(B^[I]); { Param. perturbé } Y1 := RegFunc(X, B); D^[I] := (Y1 - Y) / (B^[I] - Temp); { Dérivée } B^[I] := Temp; { Restaurer param. } end; end; procedure ApproxFit; Cette procédure calcule les estimations initiales des paramètres, avant leur affinement par la méthode de Marquardt : Pour une somme d'exponentielles, on utilise un algorithme décrit par R. GOMENI et C. GOMENI (Comput. Biol. Med., 1979, 9, 39-48). Cet algorithme comporte 3 étapes : Calcul des 2m paramètres p0, ..., p2m-1 (m étant le nombre d'exponentielles) par régression linéaire appliquée à l'équation suivante : 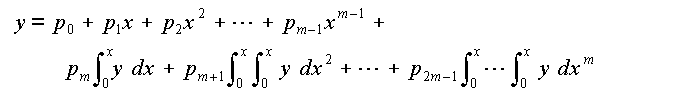Les intégrales sont évaluées par la méthode des trapèzes, après un éventuel changement d'axes pour amener l'abscisse du premier point à zéro, et soustraction d'un éventuel terme constant Ymin (estimé à 90% de la plus petite valeur de y). Les m exposants (a, b, c...) des exponentielles sont les solutions de l'équation : 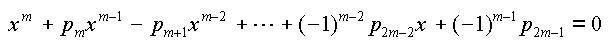Cette équation est résolue au moyen de la fonction RootPol3 de l'unité POLYNOM.PAS. Un code d'erreur (NO_REAL_ROOT) est retourné si l'équation ne possède pas m racines réelles. Une fois les exposants connus, les m coefficients (A, B, C...) s'en déduisent par régression linéaire sur les termes exponentiels : 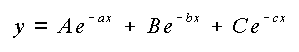Pour les deux étapes de régression linéaire, la pondération appliquée est celle définie par VarFunc. Pour une fraction rationnelle, on utilise la forme linéarisée de la fonction : 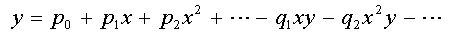  function PlotRegFunc(X : Float) : Float; Cette fonction définit l'équation de la courbe à tracer. Bien qu'elle soit en fait identique à la fonction RegFunc, elle doit faire l'objet d'une déclaration indépendante car elle n'admet qu'un seul paramètre X qui représente l'abscisse du point à tracer. Les autres parmètres (ici le vecteur B) sont déclarés comme variables globales. La fonction doit être compilée en mode FAR ($F+). {$F+} function PlotRegFunc(X : Float) : Float; begin PlotRegFunc := RegFunc(X, B); end; {$F-} L'adresse de cette fonction est passée à la procédure de tracé (PlotFunc, définie dans l'unité PLOT.PAS) par l'intermédiaire de la variable globale PlotFuncAddr : PlotFuncAddr := @PlotRegFunc; procedure ReadInputFile; Cette procédure lit le fichier d'entrée. C'est un fichier ASCII dont la structure est la suivante : ligne 1 : titre de l'étude ligne 2 : nombre de variables (doit être égal à 2 ici) lignes 3 à (M + 2) : noms des variables (un nom par ligne) ligne (M + 3) : nombre d'observations (N) lignes suivantes : tableau des variables (une variable par colonne, une observation par ligne) Les fichiers suivants sont des exemples de fichiers d'entrée : IV2.DAT, ORAL1.DAT, ORAL2.DAT pour les sommes d'exponentielles ENZYME.DAT pour les fractions rationnelles Après lecture du nombre d'observations (N), les tableaux contenant les données sont dimensionnés à l'intérieur de la procédure : DimVector(X, N); DimVector(Y, N); function LS_ObjFunc(B : PVector) : Float; C'est la fonction objectif à minimiser (c'est-à-dire ici la somme des carrés des écarts). Elle doit être compilée en mode FAR ($F+). Conformément à sa déclaration dans l'unité OPTIM.PAS, elle n'admet qu'un seul paramètre B qui représente les coordonnées du minimum (c'est-à-dire ici les paramètres de la régression). Les autres paramètres doivent être déclarés comme variables globales. procedure LS_HessGrad(B : PVector; Lbound, Ubound : Integer; G : PVector; H : PMatrix); Cette procédure calcule le vecteur gradient et la matrice hessienne de la fonction objectif (en fait &frac12;H et &frac12;G, comme expliqué en I.B.1) par un appel à la procédure DerivProc. Comme pour la fonction précédente, la liste des paramètres est fixée par la déclaration de la procédure dans l'unité OPTIM.PAS. Cette procédure doit également être compilée en mode FAR. procedure FitModel; Cette procédure effectue les calculs de régression non linéaire : Calcul des paramètres approchés au moyen de la procédure ApproxFit. Calcul des poids au moyen de la fonction VarFunc : for K := 1 to N do W^[K] := 1.0 / VarFunc(Y^[K]); Appel de la procédure de minimisation (Marquardt, définie dans l'unité OPTIM.PAS). Les adresses de la fonction LS_ObjFunc et de la procédure LS_HessGrad sont passées par l'intermédiaire des variables globales ObjFuncAddr et HessProcAddr (également définies dans OPTIM.PAS) : ObjFuncAddr := @LS_ObjFunc; HessProcAddr := @LS_HessGrad; ErrCode := Marquardt(B, Lbound, Ubound, ITMARQ, TOLMARQ, F_min, V); La signification des paramètres est la suivante : En entrée --------------------------------------------------------- B = Valeurs approchées des paramètres de la régression Lbound = Indice du premier paramètre ajusté Ubound = Indice du dernier paramètre ajusté ITMARQ = Nombre maximal d'itérations TOLMARQ = Erreur relative tolérée sur les paramètres En sortie --------------------------------------------------------- B = Valeurs affinées des paramètres F_min = Valeur de la fonction objectif V = Inverse de la matrice hessienne Test du résultat et obtention des valeurs calculées de Y : case ErrCode of MAT_OK : for K := 1 to N do Ycalc^[K] := RegFunc(X^[K], B); MAT_SINGUL : { Matrice hessienne singulière }; BIG_LAMBDA : { Le paramètre de Marquardt a été augmenté au-delà de sa valeur limite }; NON_CONV : { Le nombre d'itérations dépasse ITMARQ }; end;   procedure WriteOutputFile; Cette procédure écrit le fichier de sortie. Le nom de ce dernier correspond à celui du fichier d'entrée, avec l'extension .OUT C'est à ce niveau que se font les tests de qualité de l'ajustement et les tests des paramètres : WRegTest(Y, Ycalc, W, N, Lbound, Ubound, V, Test); ParamTest(B, V, N, Lbound, Ubound, S, T, Prob); Rappel : La procédure RegTest (ou WRegTest) doit toujours être appelée avant la procédure ParamTest, afin de calculer la matrice de variance-covariance V. procedure PlotGraph; Cette procédure trace les points expérimentaux et la courbe calculée. Elle utilise plusieurs fonctions et procédures de l'unité PLOT.PAS : AutoScale pour déterminer l'échelle des axes. GraphOk pour passer au mode graphique et tracer les axes. PlotCurve pour tracer les points expérimentaux. PlotFunc pour tracer la fonction ajustée (en utilisant la fonction PlotRegFunc définie précédemment). Dans FITEXPO la courbe est tracée avec une échelle logarithmique en ordonnée. Cela s'obtient au moyen de l'instruction : YAxis.Scale := LOG_SCALE; utilisé avant l'appel de PlotGraph.   II.C. Adaptations possibles II.C.1. Changement des fonctions de régression ou de variance Les procédures suivantes devront être adaptées si l'on change la fonction de régression : ReadCmdLine (uniquement si la fonction dépend de paramètres supplémentaires qui doivent être passés sur la ligne de commande, par exemple le nombre d'exponentielles dans le cas de l'ajustement d'une somme d'exponentielles). FuncName FirstParam LastParam ParamName RegFunc DerivProc (pas nécessaire si l'on utilise une procédure générale de dérivation numérique, telle que celle décrite précédemment) ApproxFit   Si l'on change le modèle de variance tout en gardant la même fonction de régression, seule la fonction VarFunc doit être modifiée. II.C.2. Changement de l'algorithme de minimisation En cas de non-convergence de la méthode de Marquardt, il peut être utile de changer d'algorithme de minimisation. La méthode du simplexe de Nelder et Mead (Comput. J., 1964, 7, 308-313) constitue souvent une bonne alternative. Cet algorithme est programmé dans l'unité OPTIM.PAS. Il n'utilise pas les dérivées de la fonction objectif. La procédure LS_HessGrad doit donc être appelée explicitement afin de calculer la matrice hessienne, qui est ensuite inversée au moyen de la fonction InvMat, définie dans l'unité MATRICES.PAS La procédure FitModel doit donc être modifiée comme suit : procedure FitModel; { Définir le nombre maximal d'itérations et la précision requise. Noter que la méthode du simplexe peut demander plus d'itérations que la méthode de Marquardt } const ITSIMP = 1000; TOLSIMP = 1E-4; { Déclarer et dimensionner le vecteur gradient et la matrice hessienne (pas nécessaire avec Marquardt car ces tableaux sont dimensionnés dans la procédure) } var G : PVector; H : PMatrix; ................................. begin ................................. DimVector(G, Ubound); DimMatrix(H, Ubound, Ubound); ................................. ObjFuncAddr := @LS_ObjFunc; ErrCode := Simplex(B, Lbound, Ubound, ITSIMP, TOLSIMP, F_min); case ErrCode of MAT_OK : begin LS_HessGrad(B, Lbound, Ubound, G, H); ErrCode := InvMat(H, Lbound, Ubound, V); case ErrCode of MAT_OK : for K := 1 to N do Ycalc^[K] := RegFunc(X^[K], B); MAT_SINGUL : { Matrice hessienne singulière }; end; end; NON_CONV : { Le nombre d'itérations dépasse ITSIMP }; end; ................................. end; III. Exemples Nous donnons ici 2 exemples de régression non linéaire empruntés aux domaines de la Pharmacocinétique et de l'Enzymologie : Ajustement d'une somme d'exponentielles : Concentration plasmatique d'un médicament en fonction du temps, après administration orale (Fichiers ORAL1.DAT, ORAL2.DAT) ou intra-veineuse (Fichier IV2.DAT).   Ajustement d'une fraction rationnelle : Activité d'une enzyme en fonction de la concentration du substrat (Fichier ENZYME.DAT) Remarques : Nous utilisons ici la régression non pondérée, obtenue en faisant VarFunc := 1 dans FITEXPO et FITFRAC. Les paramètres de chaque programme peuvent être saisis sur la ligne de commande du DOS (après compilation en fichier .EXE) ou dans l'option "Parameters" de l'environnement intégré. L'ajustement (non pondéré) des sommes d'exponentielles peut aussi se faire avec le logiciel WinReg qui possède une interface conviviale et de meilleures possibilités graphiques. Des programmes de Pharmacocinétique plus spécifiques sont disponibles dans la bibliothèque TP-PHARM. III.A. Concentration d'un médicament en fonction du temps Les données proviennent de l'ouvrage de Gibaldi et Perrier (Pharmacokinetics, 2nd edition, Dekker 1982). Nous utiliserons comme exemple le fichier ORAL2.DAT. On montrerait, au moyen des graphiques et des critères r2a et F, que le meilleur ajustement est obtenu avec un modèle à 3 exponentielles sans terme constant. On lance donc le programme par : FITEXPO ORAL2 3 On obtient le fichier de sortie suivant (Fichier ORAL2.OUT) : ========================================================================= Data file : ORAL2.DAT Study name : Oral - 2 comp. x variable : Time y variable : Concentration Function : y = A.exp(-a.x) + B.exp(-b.x) + C.exp(-c.x) ------------------------------------------------------------------------- Parameter Est.value Std.dev. t Student Prob(>|t|) ------------------------------------------------------------------------- A -124.6229 0.9374 -132.94 0.0000 a 0.4793 0.0025 188.79 0.0000 B 89.4276 0.5411 165.28 0.0000 b 0.1197 0.0020 59.48 0.0000 C 35.1908 0.9746 36.11 0.0000 c 0.0298 0.0005 55.85 0.0000 ------------------------------------------------------------------------- Number of observations : n = 15 Residual error : s = 0.0540 Coefficient of determination : r2 = 1.0000 Adjusted coeff. of determination : r2a = 1.0000 Variance ratio (explained/resid.) : F = 456548.8555 Prob(>F) = 0.0000 ------------------------------------------------------------------------- i Y obs. Y calc. Residual Std.dev. Std.res. ------------------------------------------------------------------------- 1 4.7000 4.6581 0.0419 0.0540 0.7758 2 13.2000 13.2163 -0.0163 0.0540 -0.3021 3 20.8000 20.8328 -0.0328 0.0540 -0.6071 4 36.3000 36.3213 -0.0213 0.0540 -0.3944 5 61.4000 61.3500 0.0500 0.0540 0.9260 6 68.1000 68.1102 -0.0102 0.0540 -0.1886 7 61.1000 61.1414 -0.0414 0.0540 -0.7675 8 52.1000 52.0859 0.0141 0.0540 0.2612 9 37.3000 37.2415 0.0585 0.0540 1.0840 10 27.5000 27.5250 -0.0250 0.0540 -0.4631 11 21.1000 21.1741 -0.0741 0.0540 -1.3732 12 16.9000 16.8431 0.0569 0.0540 1.0548 13 11.4000 11.4152 -0.0152 0.0540 -0.2810 14 8.2000 8.1437 0.0563 0.0540 1.0433 15 5.9000 5.9444 -0.0444 0.0540 -0.8231 ========================================================================= On constate que : r2 et r2a sont pratiquement égaux à 1 et F a une valeur très élevée, ce qui témoigne d'un excellent ajustement de la fonction aux points expérimentaux. L'écart-type résiduel est estimé à 0.054. Ceci correspond à un coefficient de variation compris entre 0.08% (pour y = 68.1) et 1.15% (pour y = 4.7), ce qui témoigne d'une excellente précision de la technique d'analyse. Les résidus normalisés (Std.res. = Standardized residuals) ont tous des valeurs absolues inférieures à 1.4 (pas de point aberrant), et leur répartition semble aléatoire. Chaque paramètre diffère significativement de zéro (p < 10-4). La courbe en coordonnées semi-logarithmiques (Figure 2) confirme l'excellent ajustement obtenu.   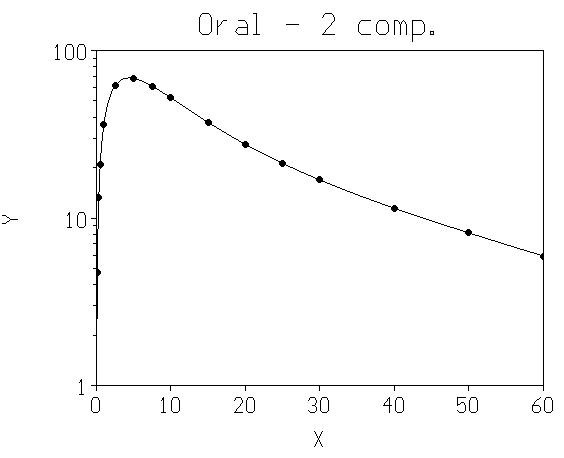Figure 2 : Concentration d'un médicament en fonction du temps III.B. Activité d'une enzyme en fonction de la concentration du substrat Nous utiliserons les données du fichier ENZYME.DAT qui représentent la vitesse initiale (v0) d'une réaction enzymatique en fonction de la concentration initiale (s0) du substrat. Ce type de relation est habituellement modélisé par des fractions rationnelles. On montrerait, au moyen des graphiques et des critères r2a et F, que le meilleur ajustement est obtenu avec un numérateur et un dénominateur de degré 2, sans terme constant au numérateur. On lance donc le programme par : FITFRAC ENZYME 2 2 Les résultats sont les suivants : ========================================================================= Data file : ENZYME.DAT Study name : Enzyme kinetics x variable : s0 y variable : v0 Function : y = (p1.x + p2.x^2) / (1 + q1.x + q2.x^2) ------------------------------------------------------------------------- Parameter Est.value Std.dev. t Student Prob(>|t|) ------------------------------------------------------------------------- p1 0.6874 0.0904 7.61 0.0000 p2 0.2157 0.1212 1.78 0.1056 q1 4.1815 0.9754 4.29 0.0016 q2 0.7370 0.4254 1.73 0.1139 ------------------------------------------------------------------------- Number of observations : n = 14 Residual error : s = 0.0055 Coefficient of determination : r2 = 0.9878 Adjusted coeff. of determination : r2a = 0.9842 Variance ratio (explained/resid.) : F = 724.8827 Prob(>F) = 0.0000 ------------------------------------------------------------------------- i Y obs. Y calc. Residual Std.dev. Std.res. ------------------------------------------------------------------------- 1 0.0531 0.0582 -0.0051 0.0055 -0.9199 2 0.0907 0.0886 0.0021 0.0055 0.3754 3 0.1250 0.1214 0.0036 0.0055 0.6460 4 0.1560 0.1526 0.0034 0.0055 0.6141 5 0.1690 0.1698 -0.0008 0.0055 -0.1451 6 0.1780 0.1818 -0.0038 0.0055 -0.6772 7 0.1840 0.1909 -0.0069 0.0055 -1.2523 8 0.2220 0.2189 0.0031 0.0055 0.5555 9 0.2410 0.2342 0.0068 0.0055 1.2243 10 0.2470 0.2441 0.0029 0.0055 0.5188 11 0.2560 0.2636 -0.0076 0.0055 -1.3739 12 0.2660 0.2719 -0.0059 0.0055 -1.0672 13 0.2780 0.2765 0.0015 0.0055 0.2653 14 0.2850 0.2795 0.0055 0.0055 0.9985 ========================================================================= On constate que : Les valeurs de r2, r2a et F sont tout-à-fait acceptables. L'écart-type résiduel est estimé à 0.0055. Ceci correspond à un coefficient de variation compris entre 1.9% (pour y = 0.285) et 10.4% (pour y = 0.0531). Cette précision, quoique faible, est compatible avec la précision habituelle des analyses enzymatiques. Les résidus normalisés (Std.res. = Standardized residuals) ont tous des valeurs absolues inférieures à 1.3 (pas de point aberrant), et leur répartition semble aléatoire. Les coefficients des termes du second degré (p2 et q2) ne sont significatifs qu'au risque 10%. Cependant la suppression de l'un d'entre eux fait diminuer les valeurs de r2a et F. Il semble donc préférable de les conserver, malgré leur faible précision. (Notons aussi que l'estimation de la précision de ces coefficients peut être erronée si leur distribution ne suit pas exactement la loi de Student). 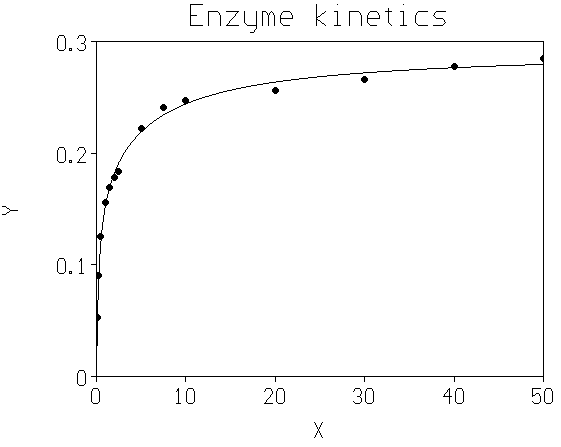La figure suivante montre la courbe obtenue :   Figure 3 : Activité enzymatique en fonction de la concentration du substrat

Informations sur l'auteur: E-mail: jdebord@MicroNet.fr Page Web: http://ourworld.compuserve.com/homepages/JDebord